A&C_task 1.6

Tasks

现有一探测器用于测量宇宙线事例，已知触发率约为60 Hz，而探测器的死时间为 3 ms，求事例堆积的概率
下面代码给定一宇宙线的触发事例能谱，以及从中挑选满足一定条件的用于分析的事例能谱，画出不同能段的效率

示例代码：

void test(){
int num=100;

//存储的原始触发事例能谱 bin 从 0-100
TH1D* all=new TH1D("all","all entries",num,0,num);

//挑选好的事例能谱
TH1D* sel=new TH1D("sel","select entries",num,0,num);

for(int i=0;i<num;++i){
int raw_temp=int(gRandom->Gaus(0,6))+200;
all->SetBinContent(i+1,raw_temp);
int temp=(1-i*0.007)*gRandom->Uniform(0.8,1.)*raw_temp;
sel->SetBinContent(i+1,temp);
}
}

优化上次作业的代码，绘出经过增益标定前后总能谱的变化，用以证明增益标定结果的准确性
*（选做题）已知上次作业能谱中第一个峰为单电荷的峰，增益标定的原理是什么？用第一个峰可能存在哪些问题？根据图中数据寻找改进的办法

One Possible Solution

Task 1

可以先简单地对事件堆积进行介绍。事件堆积指的是在某次实验中，由于粒子探测器的分辨率有限，不能分辨出几个在极短时间内同时发生的几个时间的情况，导致不同事件的信号相互重叠。这种事件常见于高探测频率或者说高粒子碰撞率的实验中，例如在LHC或者某些高亮度的探测实验中。这些实验的典型共同之处就是产生的粒子频率特别高，多个粒子事件会在短时间内产生，并同时到达探测器。由于之前提到的探测器的分辨率有限，于是无法在时间上准确识别这些不同的事件，于是会导致它们的信号混合在一起，产生“事件堆积”。

事件堆积可以分为时域堆积和空域堆积两大类。时域堆积和空域堆积的区别点实际在于事件发生的时间和探测器的响应过程之间的关系。时域堆积的简单描述是两个或多个事件几乎发生在同一时间，由于探测器的分辨率不足导致的堆积；空域堆积的简单描述是两个或多个事件发生的间隔十分相近，由于探测器的死时间或者较长读出时间的因素导致的事件堆积。二者看上去十分相似，不过它们有一个本质的不同：时域堆积中，两个事件发生在同一个时间窗内，例如通常在一次粒子束撞击或一次触发过程中，由于这些事件发生的时间间隔太近，从而在分辨率上导致事件堆积；空域堆积中，事件实际上发生在不同的时间窗口内，它们的时间间隔一般比时域堆积更长，但是由于探测器有较长的死时间或者读出时间时，会导致事件堆积。换句话说，它的关键特征是探测器还在处理前一个事件时，新的事件已经发生了，导致时间上（时间窗上）分开的不同信号被堆积认为成同一个信号。例如，当一个粒子穿过探测器后，探测器还在收集和处理信号，而第二个粒子在探测器恢复之前已经穿过了探测器，这就会导致信号重叠；死时间的情况也是类似的，只不过此时不会导致“堆积”，而是会产生遗漏，不过我们依然称它为事件堆积。

为了计算事件堆积的效率，可以利用探测器的死时间和触发率计算。在这里我们采用泊松分布。对于泊松过程，在时间内没有事件发生的概率为，所以堆积效率可以用以下公式得到：

其中是事件的触发率，即每秒发生事件的频率；是探测器的死时间；是堆积事件的概率，即在探测器死时间内有新的事件发生的概率。现在，只需要带入公式就可以得到事例堆积的概率

Task 2

在该任务中，我们使用gRandom -> Gaus(0, 10) 生成一个高斯分布的随机数（再进行平移），用于模拟每个 bin 的事件数，被赋值到all直方图的第i+1个 bin 中。然后，我们使用

int temp = (1 - i * 0.007) * gRandom -> Uniform(0.8, 1.0) * raw_temp;

对所有数据进行筛选。注意到，其中的(1 - i * 0.007) 是一个线性衰减因子。随着i的增加，该因子逐渐减小。对于较高的 bin，因子会较小，导致该 bin 中的事件数减少。另外，其中的gRandom部分引入了一定的波动性，用来模拟随机效应。最后，筛选出的数据被填入sel中的直方图中。事实上，这样的线性衰减因子用于模拟高能区的严格探测条件或者更低的探测效率。

最后一部分，计算筛选事件与原始事件的比值，得到该能段的效率。

代码如下：

void btask1_6(){
    
    int num = 100;

    TH1D *all = new TH1D("all", "All Entries; Bins; Counts", num, 0, num);
    TH1D *sel = new TH1D("sel", "Selected Entries; Bin; Counts", num, 0, num);

    for (int i = 0; i < num; ++i){
        int raw_temp = int(gRandom -> Gaus(0, 10)) + 200;
        all -> SetBinContent(i + 1, raw_temp);

        int temp = (1 - i * 0.007)* gRandom -> Uniform(0.8, 1.0) * raw_temp;
        sel -> SetBinContent(i + 1, temp);
    }

    TFile *originalFile = new TFile("original_data.root", "RECREATE");
    all -> Write();
    sel -> Write();
    originalFile -> Close();
    delete all;
    delete sel;

    TFile *inputFile = new TFile("original_data.root", "READ");
    TH1D *all_hist = (TH1D*)inputFile -> Get("all");
    TH1D *sel_hist = (TH1D*)inputFile -> Get("sel");
    
    TGraph *eff = new TGraph(num);
    eff -> SetTitle("Efficiency vs Bin; Bin; Efficiency");

    for (int i = 0; i < num; ++i){
        double all_count = all -> GetBinContent(i + 1);
        double sel_count = sel -> GetBinContent(i + 1);
        double efficiency = 0;

    if (all_count > 0){
        efficiency = sel_count / all_count;
    }
    eff -> SetPoint(i, i, efficiency);
}
TCanvas *c1 = new TCanvas("c1", "Histogram Analysis", 800, 600);
double maxVal = TMath::Max(all_hist -> GetMaximum(), sel_hist -> GetMaximum());
double minVal = TMath::Min(all_hist -> GetMinimum(), sel_hist -> GetMinimum());
all_hist -> SetMaximum(maxVal * 1.2);
all_hist -> SetMinimum(minVal * 0.8);
all_hist -> SetLineColor(kBlue);
sel_hist -> SetLineColor(kRed);
all_hist -> Draw("HIST");
sel_hist -> Draw("HIST SAME");

gStyle -> SetOptStat(0);
auto legend = new TLegend(0.75, 0.75, 0.90, 0.90);
legend -> AddEntry(all_hist, "All Entries", "l");
legend -> AddEntry(sel_hist, "Selected Entries", "l");
legend -> Draw();

c1 -> SaveAs("histogram_analysis.pdf");

TCanvas *c2 = new TCanvas("c2", "Efficiency Analysis", 800, 600);
eff -> SetMarkerStyle(20);
eff -> SetMarkerSize(0.8);
eff -> SetMarkerColor(kGreen +2);
eff -> Draw("AP");

c2 -> SaveAs("efficiency_analysis.pdf");

inputFile -> Close();
delete inputFile;
delete eff;
delete c1;
delete c2;
}

输出结果如下：

所有数据 vs 选择数据

各能段效率

Task 3

代码如下：

/* 
* 注意1：在ROOT中，直方图默认与当前目录关联（例如TFile）。当关闭TFile时，与其关联的所有直方图都会被删除，如果之后需要调用的话就会产生无效的内存访问。这可能是我在运行中偶尔出现 crash 的原因。
* 注意2：在所有部分，我只计算了区间（45,80）的卡方/自由度。
*/

#include "langaufun.C" // 该函数是根据cern.root指导网页中教程中得到的，其中定义了郎道卷积高斯函数

void atask1_6() {
	auto start = std::chrono::high_resolution_clock::now(); // 记录程序运行时间

    TVirtualFitter::SetDefaultFitter("Minuit"); // **在上一次程序运行中发现无法使用 Minuit 改用 Minuit2，这一次发现无法使用 Minuit2 改用 Minuit。由于每个A_B都要提示一次（1152次），于是预先在这里声明。但是为什么？**
    TFile *file = TFile:: Open("va.root", "READ");
    TFile *outFile = new TFile("fit_results.root","RECREATE");

    std::ofstream outputFile("chi2Ndf_and_gainCoefficients.txt");

    TH2D *gainMap = new TH2D("gainMap", "GainCoefficients; A; B", 192, 0, 192, 6, 0, 6);
    TH2D *chi2Map = new TH2D("chi2Map", "ChiSquared/NDF; A; B", 192, 0, 192, 6, 0, 6);

    double totalMPV = 0; // 用于累加MPV
    int numDetectors = 0; // 探测器数量

    std::vector<double> mpvList; // 每个探测器的MPV
    std::vector<TH1D*> correctedHists; // 输出的（校正后的）值方图
    std::vector<TH1D*> originalHists; // 由于出现了程序崩溃，存储一个原始直方图。应该是程序开头的注释中提到的问题

    int lefFit = 0, riFit = 0, lefMergedFit = 0, riMergedFit = 0; // 拟合区间
    lefFit = 45;
    riFit = 75;
    lefMergedFit = 45;
    riMergedFit = 75;

    for (int A=0; A < 192; ++A){
        for (int B=0; B < 6; ++B){
            TString histName = TString::Format("%d_%d", A, B);
            TH1D *hist = (TH1D*)file -> Get(histName);

            TH1D *histClone = (TH1D*)hist -> Clone();
            histClone -> SetDirectory(0); // 克隆后解除关联（也是为了防止读取空内存）
            histClone -> Sumw2(); // 计算误差，方便后续误差条的显示（虽然并不明显？）
            originalHists.push_back(histClone);
            // originalHists.push_back((TH1D*)hist -> Clone()); // 再次存储一个直方图

            TF1 *landauGausFit = new TF1("landauGausFit", langaufun, lefFit, riFit, 4); // 选择区间的原因在文章中有说明
            landauGausFit -> SetParameters(1.8, 50, 50000, 3);
            landauGausFit -> SetRange(lefFit, riFit);
            landauGausFit -> SetParNames("Width", "MP", "Area", "Sigma");
            landauGausFit -> SetNpx(1000); // 由于初步拟合时发现峰值附近的拟合函数看起来太尖锐，手动增加绘制精度 
            hist -> Fit(landauGausFit, "Q", "", lefFit, riFit);

            double gainCoefficient = landauGausFit -> GetMaximumX(lefFit, riFit);

            double chi2 = 0;
            int ndf = 0;
            for (int bin = hist -> FindBin(45); bin <= hist -> FindBin(90); bin ++){
            double observed = hist -> GetBinContent(bin);
            double expected = landauGausFit -> Eval(hist -> GetBinCenter(bin));
            if (expected > 0){
                chi2 += (observed - expected) * (observed - expected) / expected;
                ndf++; 
            }
            }
            ndf -= 4;

            double chi2NDF = chi2 / ndf;

            gainMap -> SetBinContent(A + 1, B + 1, gainCoefficient);
            chi2Map -> SetBinContent(A + 1, B + 1, chi2NDF);

            outputFile << A << "_" << B << " " << chi2NDF << " " << gainCoefficient << "\n";

            mpvList.push_back(gainCoefficient);
            totalMPV += gainCoefficient;
            numDetectors ++;

            hist -> Write();

        }
    }

    double targetMPV = totalMPV / numDetectors; // 计算平均值用来对齐

    for (int A = 0; A < 192; ++A){
        for (int B = 0; B < 6; ++B){

            TH1D *hist = originalHists[A * 6 + B];
            double gainCoefficient = mpvList[A * 6 + B];
            double correctionFactor = targetMPV / gainCoefficient; // 定义一个修正（对齐）因子

            TH1D * correctedHist = (TH1D*)hist -> Clone(TString::Format("corrected_%d_%d", A, B));
            correctedHist -> SetDirectory(0); // 也是解除关联
            correctedHist -> Sumw2();
            correctedHist -> Scale(correctionFactor);
            correctedHists.push_back(correctedHist);

            correctedHist -> Write();
        }
    }

    // 这是未对齐的直方图
    TH1D *mergedHistUncorrected = nullptr; // 初始化为空
    for (int A = 0; A < 192; ++A) {
        for (int B = 0; B < 6; ++B) {
            TString histName = TString::Format("%d_%d", A, B);
            TH1D *histFromFile = (TH1D*)file->Get(histName); // 直接从文件获取直方图
            
            if (A == 0 && B == 0) { // 初始创建 mergedHistUncorrected
                mergedHistUncorrected = (TH1D*)histFromFile->Clone("merged_hist_uncorrected");
                mergedHistUncorrected->Reset();
                mergedHistUncorrected->SetDirectory(0); // 解除关联
                mergedHistUncorrected->Sumw2();
            }
            mergedHistUncorrected->Add(histFromFile); // 合并数据
        }
    }

    // 这是一个用于合并的直方图
    TH1D *mergedHist = (TH1D*)correctedHists[0] -> Clone("merged_hist");
    mergedHist -> Reset();
    mergedHist -> SetDirectory(0); // 也是解除关联
    mergedHist -> Sumw2(); // 计算误差

    for (size_t i = 0; i < correctedHists.size(); ++i){
        mergedHist -> Add(correctedHists[i]);
        mergedHistUncorrected -> Add(originalHists[i]);
    }

    double bestChi2NDF = 1e6;
    int bestLefFit = 40, bestRiFit = 75;

    for (double lower = 40; lower <= 48; lower += 0.5) {
    for (double upper = 60; upper <= 75; upper += 0.5) {

    TF1 *tempFit = new TF1("tempFit", langaufun, lower, upper, 4);
    tempFit -> SetParameters(1.8, 50, 50000, 3);
    tempFit -> SetRange(lower, upper);
    tempFit -> SetParNames("Width", "MP", "Area", "Sigma");
    tempFit -> SetNpx(1000);

    mergedHist->Fit(tempFit, "Q", "", lower, upper);

    double tempChi2 = 0;
    int tempNDF = 0;
    for (int bin = mergedHist->FindBin(45); bin <= mergedHist->FindBin(80); bin++) {
        double observed = mergedHist->GetBinContent(bin);
        double expected = tempFit->Eval(mergedHist->GetBinCenter(bin));
        if (expected > 0) {
            tempChi2 += (observed - expected) * (observed - expected) / expected;
            tempNDF++;
        }
    }
    tempNDF -= 4;
    double tempChi2NDF = tempChi2 / tempNDF;

    // 判断是否为最优
    if (tempChi2NDF < bestChi2NDF) {
        bestChi2NDF = tempChi2NDF;
        bestLefFit = lower;
        bestRiFit = upper;
    }

    delete tempFit;
    }
    }

    TF1 *mergedFit = new TF1("mergedFit", langaufun, bestLefFit, bestRiFit, 4);
    mergedFit -> SetParameters(1.8, 50, 50000, 3);
    mergedFit -> SetRange(bestLefFit, bestRiFit);
    mergedFit -> SetParNames("Width", "MP", "Area", "Sigma");
    mergedFit -> SetNpx(1000);
    mergedHist -> Fit(mergedFit, "Q", "", bestLefFit, bestRiFit);

    double mergedChi2 = 0;
    int mergedNDF = 0;
    for (int bin = mergedHist -> FindBin(45); bin <= mergedHist -> FindBin(80);bin ++){
        double observed = mergedHist -> GetBinContent(bin);
        double expected = mergedFit -> Eval(mergedHist -> GetBinCenter(bin));
        if (expected > 0){
            mergedChi2 += (observed - expected) * (observed - expected) / expected;
            mergedNDF++;
        }
    }
    mergedNDF -= 4;
    
    double mergedChi2NDF = mergedChi2 / mergedNDF;

    mergedFit -> Write();
    mergedHist -> Write();
    mergedHistUncorrected -> Write();
    gainMap -> Write();
    chi2Map -> Write();
    
    file -> Close();
    outFile -> Close();
    outputFile.close();
    delete file;
    delete outFile;

    
    TFile *inFile = TFile::Open("fit_results.root", "READ");

    TH2D *gainHist = (TH2D*)inFile -> Get("gainMap"); // 增益系数热力图
    TH2D *chi2Hist = (TH2D*)inFile -> Get("chi2Map"); // 卡方分布热力图
    TH1D *mergedHistUncorrectedFromFile = (TH1D*)inFile -> Get("merged_hist_uncorrected");
    TH1D *mergedHistFromFile = (TH1D*)inFile -> Get("merged_hist"); // 合并后的直方图
    TF1 *mergedFitFromFile = (TF1*)inFile -> Get("mergedFit"); // 拟合后的合并后的直方图
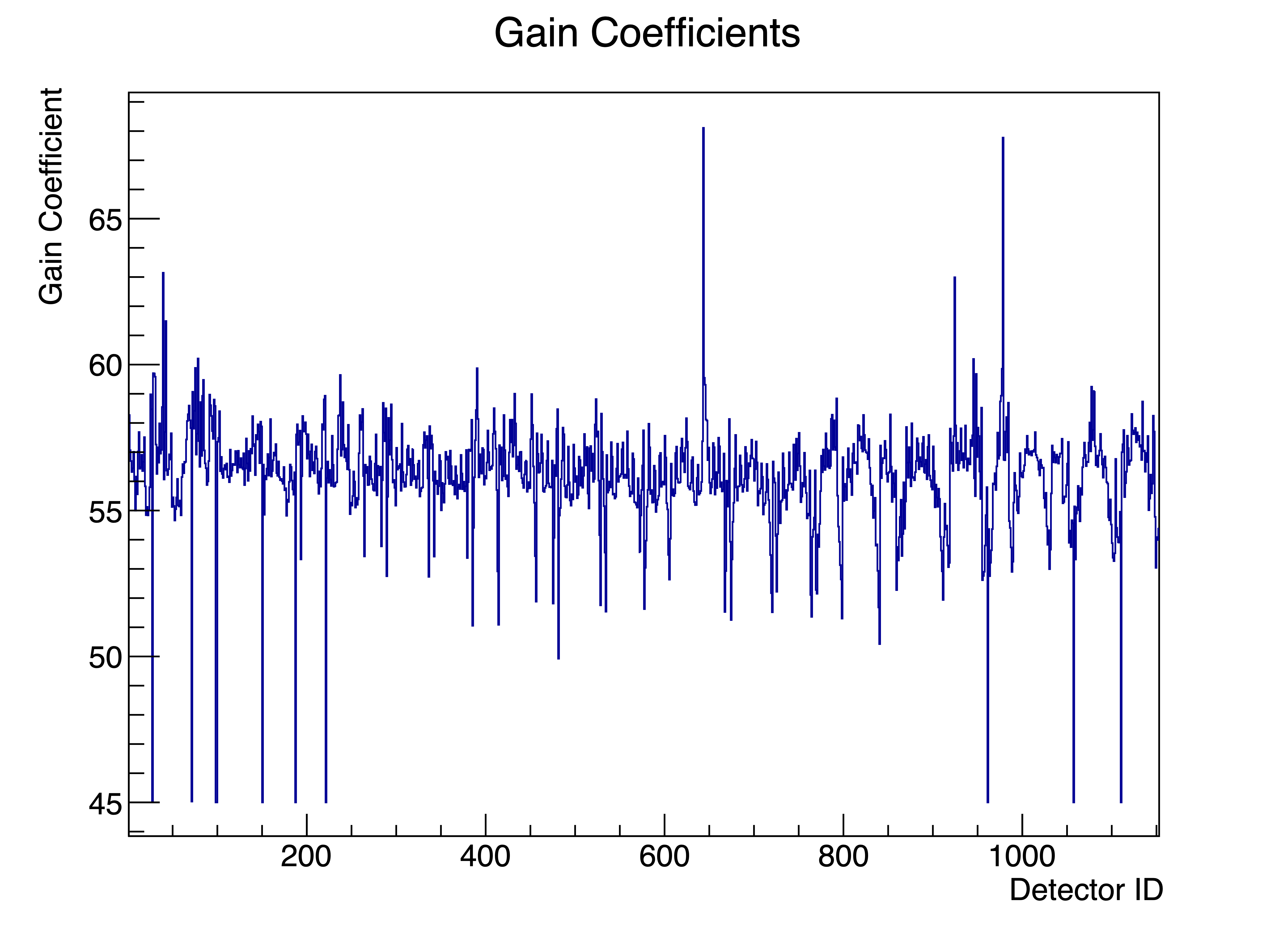
    TH1D *gainHist1D = new TH1D("gainHist1D", "Gain Coefficients; Detector ID; Gain Coefficient", 1152, 1, 1153); // 1152 bin的直方图，用于绘制增益系数

    TCanvas *c1 = new TCanvas("c1", "Gain Coefficient Heatmap", 800, 600);
    gStyle -> SetOptStat(0);
    gainHist -> Draw("COLZ");

    c1 -> SaveAs("gain_heatmap.pdf");

    TCanvas *c2 = new TCanvas("c2", "ChiSquared/NDF Heatmap", 800, 600);
    gStyle -> SetOptStat(0);
    chi2Hist -> Draw("COLZ");

    c2 -> SaveAs("chi2Ndf_heatmap.pdf");

        TCanvas *c3 = new TCanvas("c3", "Merged Spectrum Comparison", 800, 600);
    
    mergedHistUncorrectedFromFile->SetLineColor(kBlue);
    mergedHistFromFile->SetLineColor(kRed);
    
    mergedHistUncorrectedFromFile->Draw("HIST");
    double meanUncorrected = mergedHistUncorrectedFromFile->GetMean();
    double rmsUncorrected = mergedHistUncorrectedFromFile->GetRMS();
    TPaveText *statsUncorrected = new TPaveText(0.6, 0.75, 0.88, 0.85, "NDC");
    statsUncorrected->SetFillColor(0);
    statsUncorrected->AddText("Uncorrected Histogram Stats:");
    statsUncorrected->AddText(TString::Format("Mean = %.2f", meanUncorrected));
    statsUncorrected->AddText(TString::Format("RMS = %.2f", rmsUncorrected));
    statsUncorrected->Draw("SAME");

    mergedHistFromFile->Draw("SAME HIST");
    double meanCorrected = mergedHistFromFile->GetMean();
    double rmsCorrected = mergedHistFromFile->GetRMS();
    TPaveText *statsCorrected = new TPaveText(0.6, 0.6, 0.88, 0.7, "NDC");
    statsCorrected->SetFillColor(0);
    statsCorrected->AddText("Corrected Histogram Stats:");
    statsCorrected->AddText(TString::Format("Mean = %.2f", meanCorrected));
    statsCorrected->AddText(TString::Format("RMS = %.2f", rmsCorrected));
    statsCorrected->Draw("SAME");
    
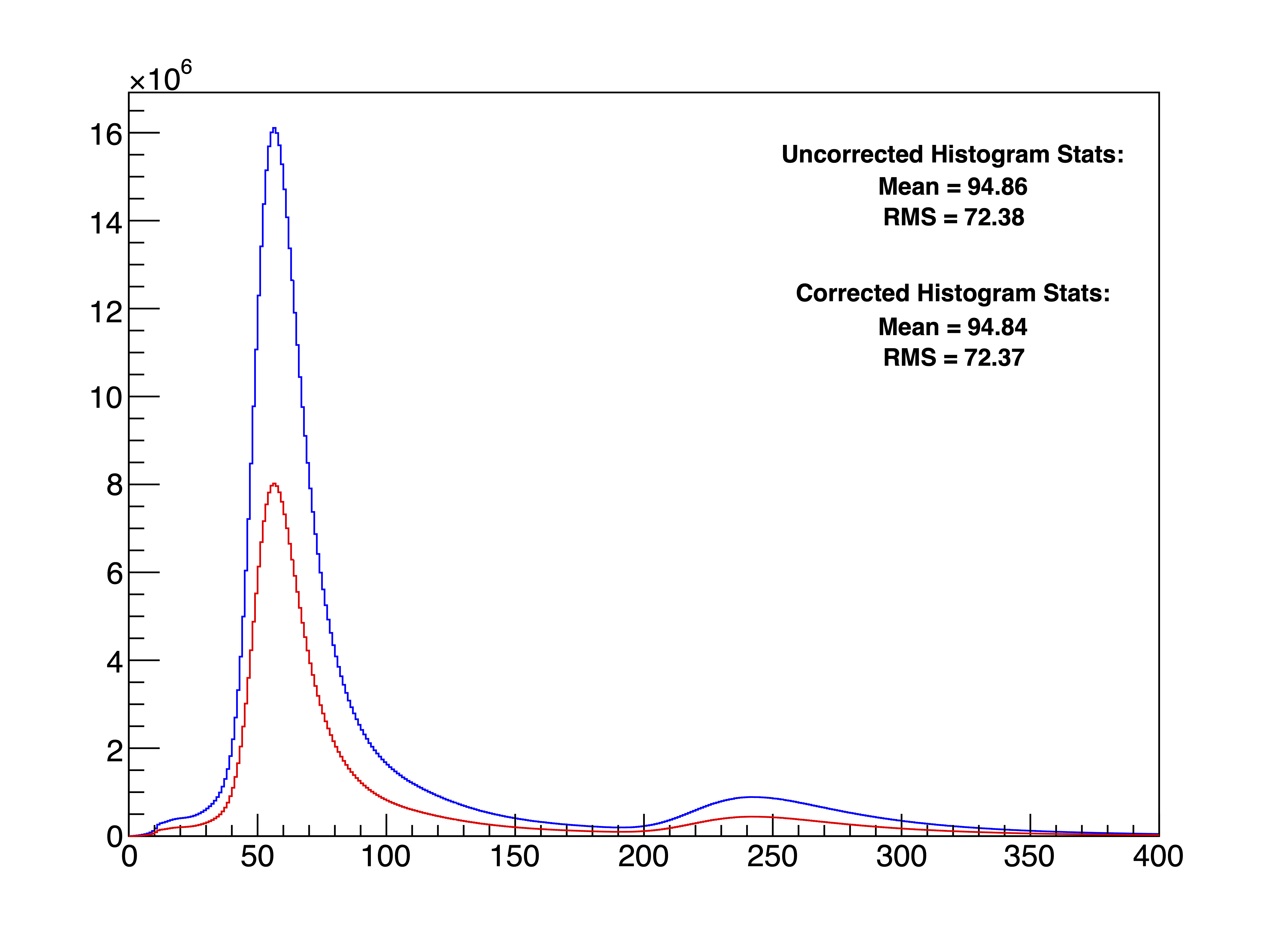
    // 这里的 merged_spectrum 实际上是对每个原始直方图进行郎道卷积高斯函数拟合，得到MPV，计算平均MPV后以 correctionFactor = targetMPV / gainCoefficient 作为校正因子对齐得到的合并的直方图
    c3 -> SaveAs("merged_spectrum_comparison.pdf");

    TCanvas *c4 = new TCanvas("c4", "Fitted Merged Spectrum", 800, 600);
    gStyle -> SetOptFit(1111); 
    mergedHistFromFile -> Draw("E1Y0");
    mergedFitFromFile -> SetLineColor(kRed);
    mergedFitFromFile -> Draw("SAME");

    gPad -> Update();
    TPaveStats *stats = (TPaveStats*)mergedHistFromFile -> FindObject("stats");
    if (stats){
    stats -> SetX1NDC(0.65);
    stats -> SetY1NDC(0.65);
    stats -> SetX2NDC(0.90);
    stats -> SetY2NDC(0.90);
    stats -> SetBorderSize(1);
    stats -> AddText(TString::Format("Chi2/NDF = %.2f", mergedChi2NDF));
    }

    c4 -> SaveAs("fitted_merged_spectrum.pdf");  
    
    TCanvas *c5 = new TCanvas("c5", "Gain Coefficients 2D plot", 800, 600);
    for (int i = 0; i < 1152; ++i){
        gainHist1D -> SetBinContent(i+1, mpvList[i]);
    }
    gainHist1D -> Draw("HIST");

    c5 -> SaveAs("gain_coefficients_1D_plot.pdf");

    inFile -> Close(0);
    c1 -> Close(0);
    c2 -> Close(0);
    c3 -> Close(0);
    c4 -> Close(0);
    c5 -> Close(0);


	auto end = std::chrono::high_resolution_clock::now();
	std::chrono::duration<double> elapsed = end - start;

    std::cout << "Optimal fit range: [" << bestLefFit << ", " << bestRiFit << "], with Chi2/NDF:" << mergedChi2NDF << "." << std::endl;
    std::cout << "Attention: All Chi2 / NDF are in the range of [45, 80]." << std::endl;
    std::cout << "Total execution time: " << elapsed.count() << " seconds." << std::endl;
}

在这里只展示拟合结果、增益标定的对比和增益系数的三幅图。

修正拟合范围的拟合结果

增益标定对齐前后对比图

增益系数

通过这个增益标定前后的对比图发现，这里的蓝色曲线（未对齐的直方图）和红色曲线（对齐后的直方图）在高度上有明显差异。这里可能是校正因子所带来的影响，如果小于1的校正因子数量过多，有可能导致图像面积的大小显著减小。事实上，如果大多数探测器的原始增益低于平均值，则在应用校正因子后，红色曲线会被整体放大。如果原始增益高于平均值，则红色曲线会缩小。在此图中，红色曲线比蓝色曲线更低，表明大部分探测器可能在校正前具有较高的响应值，从而在校正后整体缩小。

可以从另外一个角度分析。在对齐的过程中，各个探测器的直方图都被缩放到相同的目标MPV（Most Probable Value）水平。因此，对齐后的曲线表现得更加“集中”，而未对齐的曲线保持了各个探测器之间的自然波动。这种集中效应可以导致对齐后的曲线在某些区域（如主峰）变得更尖锐，而在其他区域（如低尾或高尾）则变得更平缓。

不过，这样的显著差异是否合理？直观上来看，经过增益标定后的数据应该更为集中，在图像上表现为图像更窄、峰值附近更尖锐；但是该图像中几乎只有缩小，没有聚拢的表现。这是令人困惑的一点。

Task 4

这里简单回顾一下task1.4 中关于增益系数和增益标定的内容：

“另外，需要简单介绍一下题目中需要我们计算的”增益系数“。增益系数（Gain Coefficient）事实上是粒子探测器中用来描述探测器对输入信号放大能力的一个参量。具体来说，增益系数通常表示为探测器输入信号与输出信号之间的比值；在这里，给定相同的输入，可以通过拟合探测器输出的响应分布计算出探测器的增益系数。

在附件va.root中，我们有1152个TH1D类型的直方图，分别对应320微米厚硅微条探测器对粒子的响应。其中，横坐标代表输出信号，纵坐标代表事件的频率或概率。在代码中，我们采用了郎道卷积高斯函数进行拟合（参考cern.root上的教程代码进行卷积计算），其中有四个参数：

par[0]: 郎道分布的宽度参数
par[1]: 郎道分布的最可能值
par[2]: 卷积的总面积
par[3]: 高斯分布的宽度

在拟合直方图后，我们可以提取出郎道分布中的最可能值作为增益系数；因为它其实是输出响应的最可能值，能够代表探测器在接受到相同输入时，输出信号的最大值位置，能够代表每个探测器的增益系数的大小。

另外，如果希望得到更确切的MPV值，可以选择计算郎道卷积高斯分布最大值的横坐标作为MPV。在这里，我们选择这一种做法。“

以上是1.4中的介绍。增益标定通常是通过已知的单电荷信号峰来校准探测器的输出响应。简单来说就是通过对齐之前提到的MPV值的位置来得到对齐后的图像。在此过程中，探测器对单电荷粒子的响应用于设定一个基准，通过对该峰进行拟合（例如使用高斯拟合或朗道卷积高斯拟合），可以获得其位置（MPV，Most Probable Value）。增益标定系数可以根据该MPV计算出（在代码中已经体现），使得探测器输出幅度相对于输入粒子电荷量成比例。如此一来，不同探测器的响应可以归一化到同一基准，使它们对相同粒子输入产生一致的输出。由于已知其可以被认为是相同的输入，所以不再需要加权处理，只需要简单地计算增益系数即可完成标定或对齐。

事实上，使用单电荷峰标定增益具有一些缺陷。首先就是不可避免的统计误差与噪声。在大多数情况下，这些误差和噪声的影响较小，从而可以通过拟合相对准确地得到MPV的位置；但如果如果单电荷峰的信号较弱，统计误差和背景噪声会影响峰值的准确定位，导致标定的不准确。另外，我们无法总是准确地判断峰的形状和其适用的拟合函数，即峰的形状具有复杂性。单电荷峰可能受到能量损失机制（例如电离能量沉积和多次散射）的影响，导致峰形变宽或偏离理想分布，影响拟合结果的准确性。

另外，我们事实上可以从对齐后的图像中发现，探测范围内具有至少两个峰值，这可能暗示另一个电荷或粒子的存在。如果另一个信号代表另一个电荷，我们需要考虑是否单电荷峰的增益可能与多电荷峰的增益不同，单电荷峰的标定对多电荷情况下的测量是否能很好或者完全地适用。换句话说，探测器在单电荷和多电荷的响应之间可能存在非线性的关系。当然，如果多个信号的位置集中，例如如果其他峰（如高能电荷沉积）与单电荷峰接近，可能造成拟合困难或误识别，影响标定的精确度。

首先有一些简单的方法能够改善增益标定的准确性。首先就是采用更强的峰用于标定。在前面提到，使用单电荷峰标定的问题在于信号通常较弱，在某些情况下可以尝试使用多电荷峰（例如双电荷或三电荷峰）来进行标定，这样信号更强，峰位置更稳定。还可以改进拟合函数，例如我们这次使用朗道卷积高斯函数进行拟合，在不同的情况可以使用不同的函数完成拟合，尽可能优化拟合函数，增加拟合质量。事实上，可以尝试加权拟合的方法，将拟合区间扩大的同时，对单电荷峰及其周边区域施加不同的权重，增强对主峰位置的关注，减少背景的影响。

另外，如果对第二个峰的成因较清楚，或者希望进行多种尝试，可以采用多参数进行增益标定，不只关注某个峰，而是结合多个峰的位置进行标定，将单电荷与多电荷响应关联在一起，基于整个能谱的形状进行标定，从而对峰的非线性响应进行补偿。值得注意的是，其实第一个峰的左侧还有一个较小的峰值，也可以应用在增益标定中。

还可以通过不同的方法选取最优拟合区间。事实上，我们在代码中已经应用了某个最简单的遍历以寻找较优的拟合区间。在其中可以尝试机器学习等领域的方法用来寻找目标区间。

在这里的标定中，另外两个峰由于主峰的影响不太明显，有另外一个分析方法。由于我们已经得到了与主峰相对贴合的拟合函数，我们可以将该函数扩展到全范围，而后将原始数据减去该拟合数据，就可以在一定程度上去除主峰的影响。当然，反之也可以对第二个峰进行峰附近的小范围拟合，得到一个小峰的拟合函数，再将原始数据减去该函数值，这样主峰就相对而言更加完整。简单说，其实就是分别对每个峰进行分析，去除其他峰的影响。

以上是可能能够采用的标定方法。

Any%