A&C_task 1.3

Tasks

1、从下面的链接中下载root文件，打开其中的”r_strip(TH2D)”，选取X方向前5个bin，将其投影到Y方向作为新的”TH1D”，这是粒子经过300微米硅微条探测器收集到的信号，指出其服从什么分布并拟合，并以论文的标准作图。

• 提示1：投影操作选取前5个的代码为r_strip projectionY（””，5,0）
• 提示2：提示1也许不那么可靠
• 提示3：作图可以参考分享文件中”style.h”，在绘图程序中加入其头文件后

#include <YOUR_DIR/style.h>
...
void test(){
...
MyStyle();
...
}

分享文件:result.root等[批量分享]

云盘链接:https://pan.cstcloud.cn/s/vMvhmHm4TPI

过期时间:2025-09-09 16:36:03

One Possible Solution

注意：硅微条探测器的知识放在task 1.4 中展开讲解。另外，在提供的电子材料中也有相关课件与资料，详见”Beginner’s Guide：Possible Starting Pathway “部分。

首先，硅微条探测器是一种基于半导体硅材料的粒子探测器。它可以通过探测带电粒子穿过硅材料时产生的电荷进而测量粒子的路径、能量和其他相关物理量。硅微条探测器的基本工作原理依赖于硅的电离效应：当高能带电粒子穿过硅材料时，会与硅原子发生相互作用，产生电子-空穴对。这些电子和空穴在电场作用下分别向不同的电极移动，从而形成可检测的电信号。

硅微条探测器中的能量损失分布和粒子在穿越探测器时的电离过程的能量损失分布相似，这其实和上一次作业中粒子穿越不同厚度的介质产生不同电离能量损失的分布的相关。事实上，它们的原理几乎是一样的，都是依赖于粒子通过材料时产生的电离效应。不同的是，硅微条探测器将这种能量损失通过半导体中的电荷收集过程转化为可测量的电信号。题目中提到的投影到Y上的信号实际上就是粒子的能量沉积。

可以粗略地依靠直觉首先判断出投影后的结果服从何种分布。正常情况下，带电粒子穿过硅时的平均自由程通常依赖于粒子的类型、能量以及硅材料的密度。题目中没有提到被测粒子是何种粒子，可以暂且假设它不具有太高的能量。对于高能带电粒子，如质子或电子，穿过硅时的平均自由程大致在几微米到几十微米的范围内；具体数值取决于粒子的能量水平：能量越高，自由程越长。这样的硅条具有300微米的厚度，可以显然地断言我们得到的分布不应当是高斯分布或者不应当具有太对称的结构，毕竟厚度和自由程的数量级差异并不大；同时，我们也可以发现它不太应该满足完美的朗道分布，因为硅微条其实并不太薄。不过从直觉上而言，高斯分布产生的原因是大数碰撞的中心极限定理的结果，在厚度仅比自由程大一个数量级的情况下，朗道分布应当能够得到更好的拟合结果。

不过一般情况下，Vavilov修正的Landau显然能够满足大部分的分布拟合，无论是薄片还是较厚的微条，唯一的缺点就是有时可能较为复杂，不好处理。所以不妨最后再添加一个Vavilov分布的拟合，用来比较朗道分布和高斯分布在不同位置的拟合结果（例如峰值的两侧的低点，左侧可能更符合高斯分布，而右侧在朗道分布的拟合下表现可能更好。为什么？）

写出代码如下：

#include "/home/albert/rootdoc/actask3/style.h"

void task1_3(){
    
    MyStyle(); // 应该是头文件中的内容

    TFile *file = TFile::Open("result.root");
    TH2D *r_strip = (TH2D*)file ->Get("r_strip"); 

    // 先输出原有数据的图像，可以作为一个简单的快速参考
    TCanvas *c0 = new TCanvas("c0", "r_strip_output", 600, 800);
    r_strip -> Draw();

    gStyle -> SetOptStat(1111);
    r_strip -> SetStats(1);

    c0 -> SaveAs("r_strip_output.png");
    delete c0;

    TH1D *h1a = r_strip -> ProjectionY("TemTitle1", 1, 5);
    TH1D *h1b = r_strip -> ProjectionY("TemTitle2", 1, 5);
    TH1D *h1c = r_strip -> ProjectionY("TemTitle3", 1, 5);

    /*
    * 似乎调用h1a -> Fit("vavilov", "R");之后，ROOT会创建一个新的TF1对象并附加到h1a中。因此，需要使用h1a -> GetFunction("vavilov")来获取这个新的拟合对象。
	* 修改后的代码首先执行拟合操作，然后通过GetFunction()获取实际的拟合对象，再对这个对象设置参数名和其他属性。
    */

    TF1 *fitResultVavilov = new TF1("vavilov", "[0]*TMath::Gaus(x, [1], [2]) + [3]*TMath::Landau(x, [4], [5])", 0, 200); 
    fitResultVavilov -> SetParameters(1, 20, 5, 1, 10, 2);  // 初始参数
    h1a -> Fit("vavilov", "R"); // Vavilov分布拟合

    // 获取实际的拟合函数对象
    TF1 *fitResultVavilovFitted = h1a -> GetFunction("vavilov");
    fitResultVavilovFitted -> SetParName(0, "Gauss_Amplitude");
    fitResultVavilovFitted -> SetParName(1, "Gauss_Mean");
    fitResultVavilovFitted -> SetParName(2, "Gauss_Sigma");
    fitResultVavilovFitted -> SetParName(3, "Landau_Amplitude");
    fitResultVavilovFitted -> SetParName(4, "Landau_Mean");
    fitResultVavilovFitted -> SetParName(5, "Landau_Sigma");
    fitResultVavilovFitted -> SetLineColor(kBlue);

    h1b -> Fit("landau");
    TF1 *fitResultLandau = h1b -> GetFunction("landau");
    fitResultLandau -> SetLineColor(kRed);

    h1c -> Fit("gaus", "q");
    TF1 *fitResult = h1c -> GetFunction("gaus");
    fitResult -> SetLineColor(kGreen);

    // 创建 root 文件, 后续再输出图像文件
    TFile *outFile = new TFile("output1_3.root", "RECREATE"); 
    h1a -> Write();
    h1b -> Write();
    h1c -> Write();
    fitResult -> Write("gauseFit");
    fitResultLandau -> Write("landauFit");
    fitResultVavilov -> Write("vavilovFit");
    outFile -> Close();
    file -> Close();



    // 接下来通过 output1_3.root 生成输出的图片
    TFile *inFile = TFile::Open("output1_3.root");

    TH1D *h2 = (TH1D*)inFile -> Get("TemTitle1");
    TF1 *fitResult2 = (TF1*)inFile -> Get("gauseFit");
    TF1 *fitResultLandau2 = (TF1*)inFile -> Get("landauFit");
    TF1 *fitResultVavilov2 = (TF1*)inFile -> Get("vavilovFit");

    TColor *colorGray = new TColor(2000, 145/255.0, 146/255.0, 171/255.0);
    TColor *colorBlue = new TColor(2001, 99/255.0, 178/255.0, 238/255.0);
    TColor *colorRed = new TColor(2002, 248/255.0, 149/255.0, 136/255.0);
    TColor *colorGreen = new TColor(2003, 118/255.0, 218/255.0, 145/255.0);
    h2 -> SetLineColor(2000);
    fitResult2 -> SetLineColor(2001);
    fitResultLandau2 -> SetLineColor(2002);
    fitResultVavilov2 -> SetLineColor(2003);
    
    TCanvas *c1 = new TCanvas("c1", "Histogram", 800, 600);
    h2 -> GetXaxis() -> SetLabelSize(0.04);
    h2 -> GetYaxis() -> SetLabelSize(0.04);
    h2 -> Draw();
    fitResult2 -> Draw("same");
    fitResultLandau2 -> Draw("same");
    fitResultVavilov2 -> Draw("same");

    TLegend *legend = new TLegend(0.67, 0.5, 0.92, 0.63);
    legend -> AddEntry(h2, "Origin Data", "l");
    legend -> AddEntry(fitResult2, "Gaussian Fit", "l");
    legend -> AddEntry(fitResultLandau2, "Landau Fit", "l");
    legend -> AddEntry(fitResultVavilov2, "Vavilov Fit", "l");
    legend -> SetTextSize(0.03);
    legend -> Draw();

    gStyle-> SetOptStat("eMRSK");
    gStyle-> SetOptFit(); // 这样能显示所有的参数
    h2 -> SetStats(1);

    TPaveStats *stats = (TPaveStats*)h2 -> FindObject("stats");
        stats -> SetX1NDC(0.65);
        stats -> SetY1NDC(0.65);
        stats -> SetX2NDC(0.9);
        stats -> SetY2NDC(0.9);

    TLatex *title = new TLatex();
    title -> SetTextAlign(22);
    title -> SetTextSize(0.032);
    title -> DrawLatexNDC(0.495, 0.047, "Fig 1. First 5-bin Y-projection and Fitting of Particle Signal Distribution in a 300 #mum Silicon Strip Detector"); // 当然在实际撰写论文时，标题一般在word中添加而不是在图像中添加
    gPad -> Update();

    c1 -> SaveAs("task1_3_output.png");
    c1 -> SaveAs("task1_3_output.pdf");

    // 写入其余两个函数拟合的统计值用于对比
    ofstream outfile("fit_statistics.txt");

    outfile << "Gaussian Fit Results:\n";
    outfile << "Amplitude: " << fitResult2->GetParameter(0) << " ± " << fitResult2->GetParError(0) << "\n";
    outfile << "Mean: " << fitResult2->GetParameter(1) << " ± " << fitResult2->GetParError(1) << "\n";
    outfile << "Sigma: " << fitResult2->GetParameter(2) << " ± " << fitResult2->GetParError(2) << "\n";
    outfile << "Chi-square: " << fitResult2->GetChisquare() << "\n";
    outfile << "NDF: " << fitResult2->GetNDF() << "\n\n";

    outfile << "Landau Fit Results:\n";
    outfile << "Amplitude: " << fitResultLandau2->GetParameter(0) << " ± " << fitResultLandau2->GetParError(0) << "\n";
    outfile << "MPV: " << fitResultLandau2->GetParameter(1) << " ± " << fitResultLandau2->GetParError(1) << "\n";
    outfile << "Sigma: " << fitResultLandau2->GetParameter(2) << " ± " << fitResultLandau2->GetParError(2) << "\n";
    outfile << "Chi-square: " << fitResultLandau2->GetChisquare() << "\n";
    outfile << "NDF: " << fitResultLandau2->GetNDF() << "\n";

    outfile.close();
}

[Question：如何指定在图例中显示Vavilov分布的拟合统计数据？]

因为同时显示三个拟合数据会让绘制的图像显得杂乱，所以我希望在图例中显示且仅显示Vavilov分布的拟合统计数据，不过一直没有找到方法。但是我发现，默认的输出拟合数据是第一个进行拟合的函数的数据，所以我能够通过调整 p class='h1'a h1b h1c对应的拟合函数更换需要统计的函数，并且选择在txt中输出其它的参数。不过必然有简单的方法，是什么方法？

代码输出了两个结果：

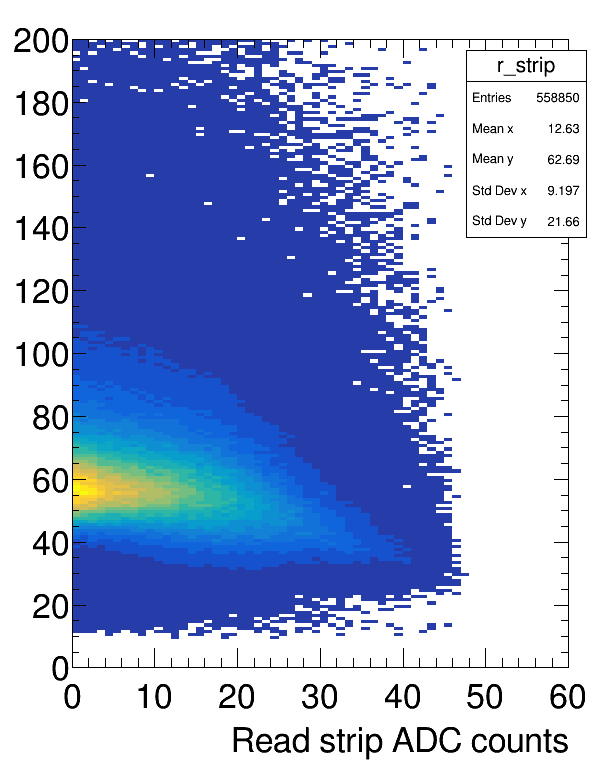
第一幅图粗略地生成了所给源数据中的二维分布。很明显地看到它具有偏态分布（虽然并没有给出color bar）。

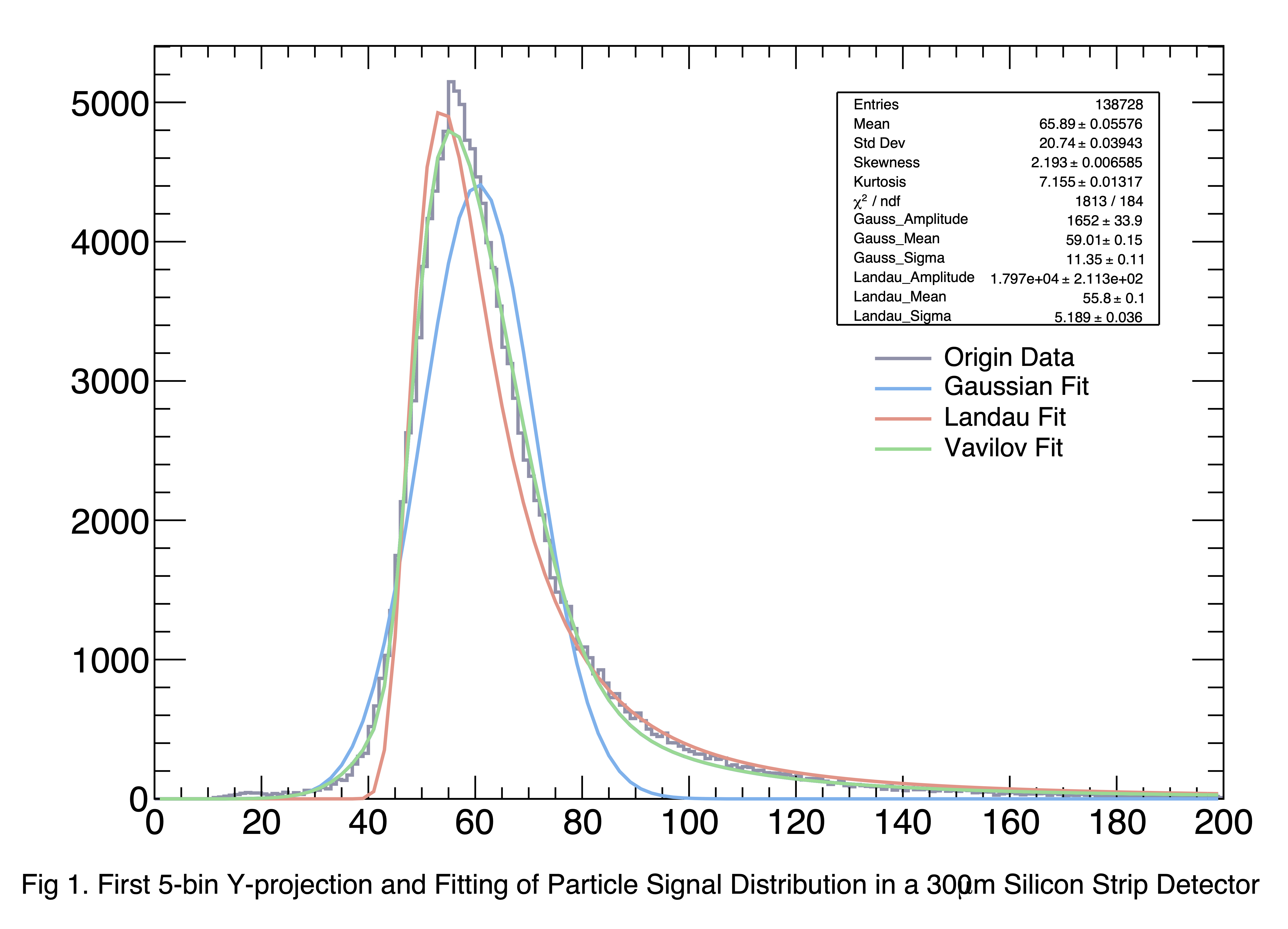
第二幅图给出了前5个bin在Y轴的TH1D投影，同样可以观察出偏态分布的痕迹（注意：图中的拟合统计数据是Vavilov分布的数据；其它两条曲线在后文中输出为txt文件供比较。）。不过注意峰值两侧的底端变化，左侧的变化较为平滑，不如朗道分布的左侧阶梯骤升；右侧的变化较为平缓，不如高斯分布的骤降（当然可以直接联想到高斯分布的原理，所有合理的分布点都位于的范围内，不具备偏态分布的长尾巴。）因此可以断定，虽然数据点具有很明显的偏态分布（甚至可以直接说朗道分布）特征，但是在一些局部不能简单地使用高斯分布或者朗道分布来进行拟合。

于是代码中分别将高斯分布、朗道分布与Vavilov分布进行了拟合，得到了不同颜色的三条曲线。能够很明显地看出上一段提到的三点内容：左侧服从高斯分布，右侧服从朗道分布，而峰值服从朗道分布的偏态性（当然，位于高斯分布和朗道分布的两峰之间！）。

比较原始数据曲线和Vavilov分布，我们可以发现，Vavilov分布几乎在所有部分很完美地拟合了数据的结果。不过唯一令人困惑的是，无论是高斯分布还是朗道分布，甚至是Vavilov分布，都不能很好地拟合峰值的结果。原始数据的峰值令人诧异地高出三个拟合曲线（为什么？可能是因为数据点较少的原因？）。

例如，这是教材中给出的电离过程分布以及拟合的朗道分布（路径很短，例如薄层气体），它在峰值处没有明显的差别：

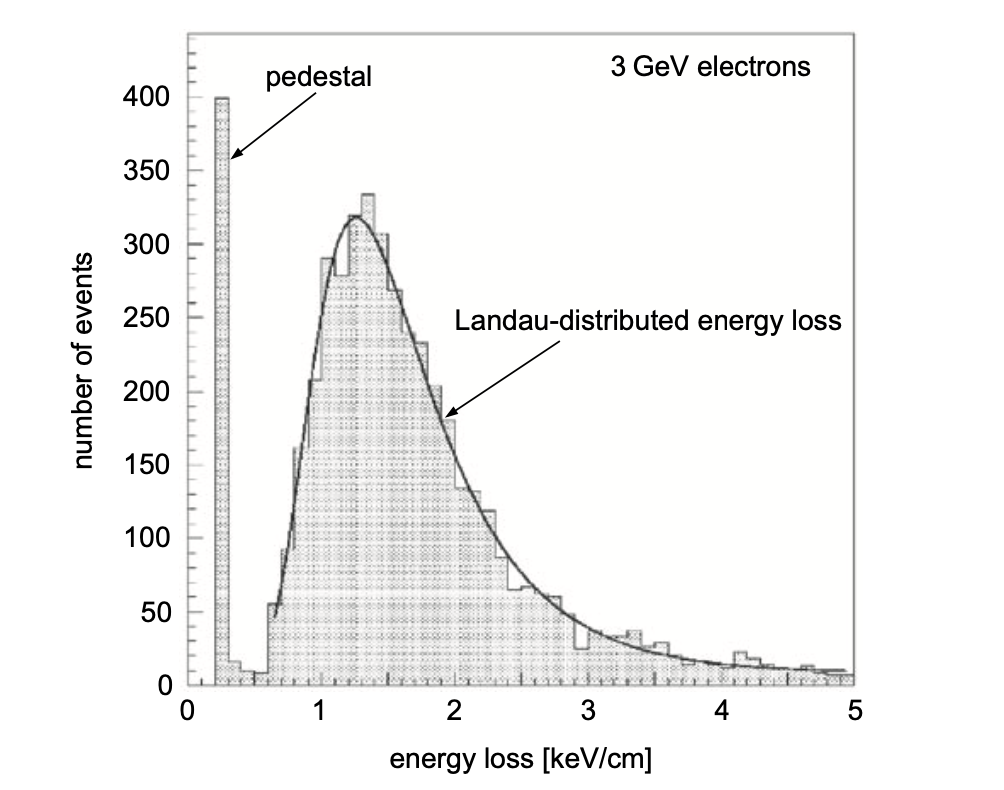
在Task1_2 中提到的这些实验中，峰值的数据点也贴合地非常完美（虽然我暂时不清楚是该论文的作者如何进行拟合的）：

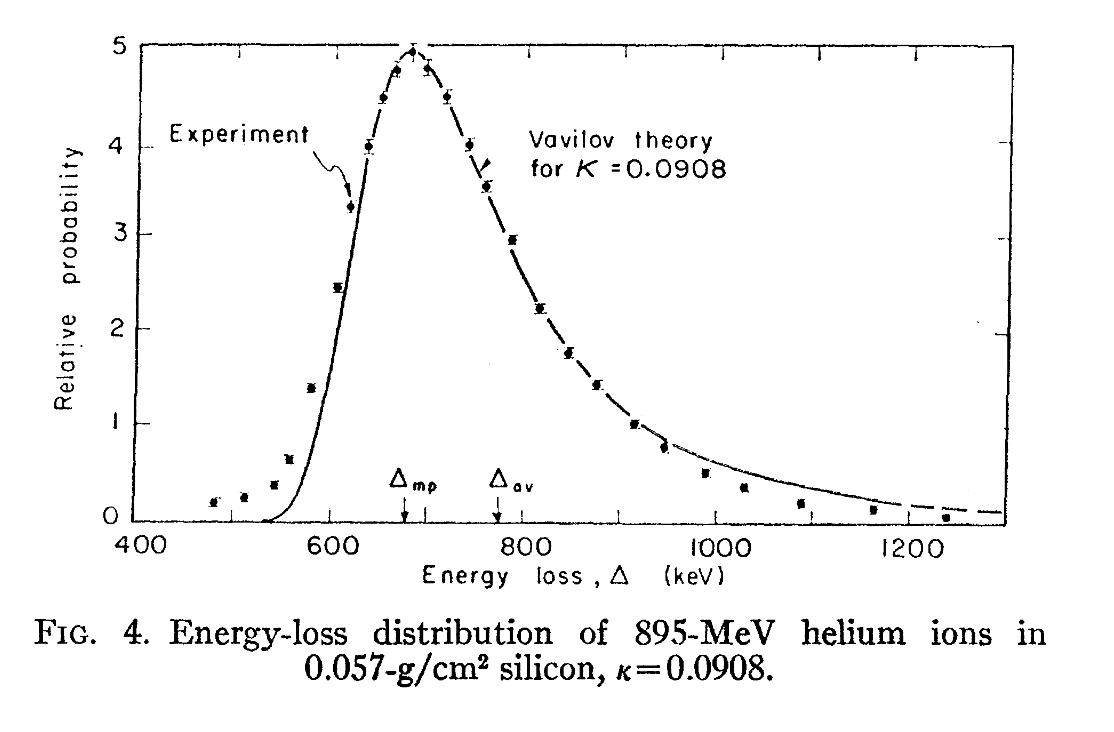
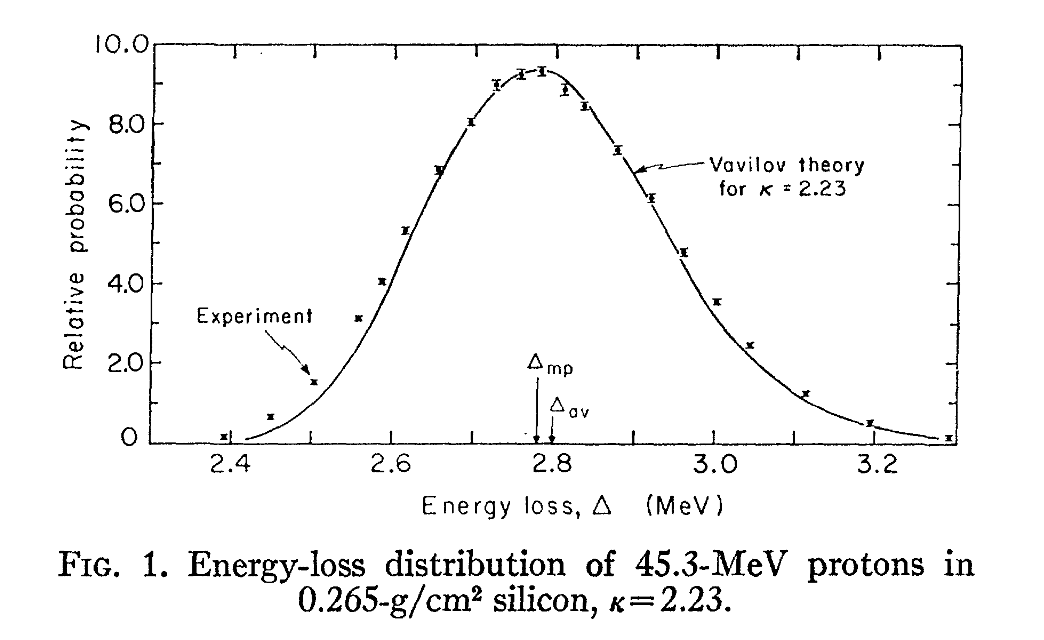
这是能量不变，将厚度增加一个数量级，偏态性明显地降低，得到的更趋向于正态分布的结果：

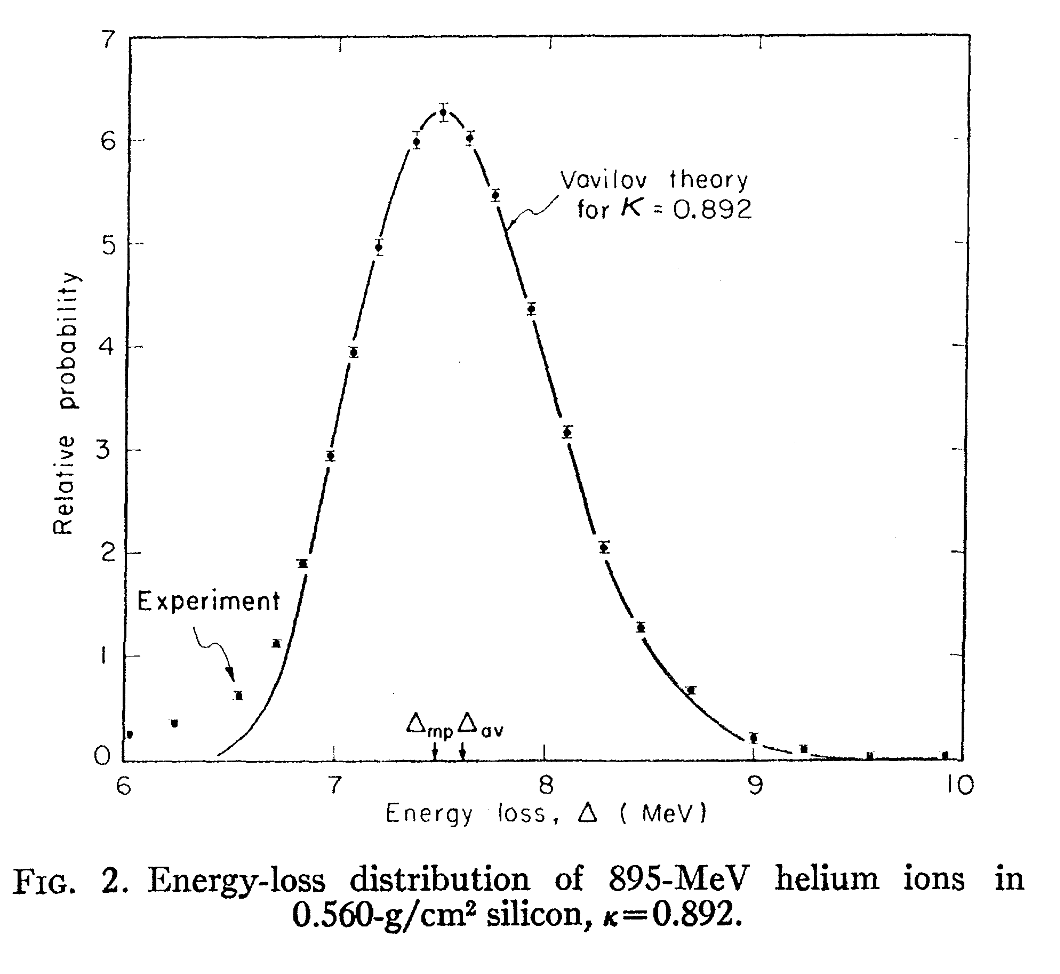
在另一种情况下，对于45.3MeV的质子，穿过0.265的硅片，得到一个几乎满足正态分布的能量损失分布：

它们也都在峰值处具有很高的精确性。

[Question：分布拟合的选择]

虽然选择了高斯、朗道和Vavilov分布进行拟合，但这些分布的物理基础和适用范围都值得深入探讨。为什么朗道分布在大部分情况下表现较好？这当然与粒子通过材料时的电离效应密切相关。而高斯分布的适用场景主要是在累积的随机过程（如碰撞次数多的情况）。Vavilov分布则提供了朗道和高斯分布之间的一个过渡区域，适用于粒子能量损失较复杂的情况。

实际操作中，使用标准的Vavilov分布或许太过麻烦；甚至我们在代码中使用的Vavilov分布也只是一种近似：我们采用的是高斯分布与朗道分布混合的公式描述Vavilov分布，而不是标准的

其中

• 是粒子在介质中损失的能量，
• 是能量损失的期望值，
• 是特征能量损失尺度，
• 表示Vavilov分布的无量纲形式。

当 很小时（），Vavilov分布趋近于Landau分布; 当 较大时（通常 ），分布逐渐接近高斯分布。

我们在代码的最后，还将高斯分布和朗道分布的统计数据输出，用于比较拟合的质量（图中显示的是Vavilov分布的统计数据）：

Gaussian Fit Results:
Amplitude: 4411.59 ± 18.5964
Mean: 60.5593 ± 0.0410882
Sigma: 10.6075 ± 0.0322276
Chi-square: 21055.5
NDF: 187

Landau Fit Results:
Amplitude: 27436.4 ± 117.785
MPV: 54.9014 ± 0.0326169
Sigma: 4.9042 ± 0.0166868
Chi-square: 8819.68
NDF: 187

根据以上数据可以发现，对于高斯分布，其卡方约为21055，而对于郎道分布而言，卡方值约为8819；而在图中输出的Vavilov分布中，卡方只有1813（事实上相当不错）。可以明显地看出，郎道分布具有比高斯分布更优秀的拟合结果，这在绘制出的图像中也可以明显地看出：橙色的郎道分布很好地贴合了数据曲线，而高斯分布的偏差比较明显。当然，最优秀的拟合结果是Vavilov分布，在图像中以绿色曲线表示：它无论是在上升与下降部分的贴合程度。还是在峰值两侧最低部分的贴合程度都十分好，唯一有缺陷的是在峰值上的贴合情况。这有可能是因为数据点较少，噪声的影响比较大（当然，具体的原因必须进一步讨论分析）。

[Question：为什么峰值附近的拟合效果较差？]

为什么峰值附近的拟合效果较差？这可能是由于噪声、探测器分辨率限制、数据量少等多种因素的共同影响。对峰值附近的数据进行进一步研究（如提高采样精度或使用不同的探测器）或许可以为实验设计提供参考。

[Question：拟合结果的物理解释]

高斯、朗道和Vavilov分布的拟合参数，如振幅、平均值（或MPV）、标准差（或宽度），可能与探测器的性能和粒子本身的物理性质或能量等运动量相对应。例如，朗道分布的最可能值（MPV）通常与粒子的能量损失密切相关，进一步分析这些参数可以帮助理解探测器对不同能量粒子的响应。特别是，我们在之前的讨论中提到了对自由程的估计–对于高能带电粒子，如质子或电子，穿过硅时的平均自由程大致在几微米到几十微米的范围内；具体数值取决于粒子的能量水平：能量越高，自由程越长。我们在估计时假定了粒子不具有太高或太低的能量，以及假定粒子可能是这里提到的电子或质子：问题是，我们在得到了实验结果，无论是图一中的二维图，还是图二中的投影图后，如何能够凭借这样的图像甚至结合不同的实验数据结果，得到对粒子种类以及能量大小估计？我们在之前提到，对于具有较低能量的同一粒子，它可能具有相对较小的自由程，从而更符合高斯分布；对于具有较高能量的粒子，它可能更符合高斯分布：这也解释了为什么我们在代码中选择了使用高斯分布和朗道分布的组合作为近似的Vavilov分布充当拟合函数，因为拟合得到的比例（权重）必然在一定程度上反映了能量的相对大小。另外，是否有可能进一步结合其它拟合参数（如朗道分布的MPV值）中定量估算粒子的能量？因此，尽管卡方能够在一定程度上很好地评估拟合的质量，对其它参数的分析也是很重要的一环。

[Question：拟合峰值的误差]

上文中已经指出了峰值拟合偏差可能是由于噪声或数据点较少。但实际上，可以进一步探讨如何减小噪声的影响。例如，是否可以通过增加数据采集点或采用更复杂的去噪算法来改善峰值附近的拟合效果？