A&C_task 1.2
Tasks
Task 1
简述插值和拟合的区别，试各举一例应用以及常见的插值和拟合的原理；ROOT使用TF1拟合默认基于什么原理，其应用的注意事项以及和极大似然之间的区别，如何评估拟合质量的优劣？
Task 2
辐射长度和核作用长度分别是什么，简单比较经过1毫米厚的碳、铝、钨板后电子的能量衰减到原来的多少，对于1GeV、10 Gev、100 GeV 的电子，经过这些这些物质时，多重散射角分别为多大？（不需要非常精确的结果）
简单介绍粒子穿过厚、薄介质时，电离能量损失的分布有何不同，为什么？
One Possible Solution
Task 1
插值通过已知的离散数据点来推测这些点之间的未知数据点，要求得到的插值函数通过所有数据点；拟合通过某种方法寻找一个目标函数或模型，能够近似表示数据趋势，但不需要通过所有数据点，通过最小化某种误差得到较优或（难以实现）最优的方案，一般得到的拟合函数不通过所有数据点。一般来说，由于插值法严格通过已知点，因此适用于精确数据，以推测未知点的数据值；拟合则允许误差的存在，适用于有噪声的或复杂的数据集，目的是捕捉数据的整体趋势。
例如，在多丝正比室（MWPC）中，阳极丝检测到离散的初步信号。在技术上，常使用插值法估计粒子通过的位置。在时间投影室（TPC）中，插值法也作为重建粒子的轨迹的重要手段。在其它领域，例如地形测绘或建模中，勘探队不可能对全部位置进行精准的测量，只能得到部分离散的点位；后续在地形重建时可能会选择使用插值法生成整个区域的地形模型，得到任意位置的高度信息。以上过程中由于噪声的影响相对较小，可以将测量值认为是真实值，于是在数据分析或轨迹重建中使用了插值法。
拟合适用于测量过程中具有噪声的情况。一般情况下，对于那些不具有特别高的测量精度的实验，以及具有可观噪声的实验数据，通常使用拟合法。通过曲线拟合，可以找到描述这些数据的数学模型，例如用最小二乘法拟合一条直线来描述两个变量之间的线性关系。在分析
在ROOT中，TF1类用于定义一维函数进行数据拟合，其默认的拟合方法基于最小二乘法，通过最小化观测数据点与拟合模型之间偏差的平方和来优化拟合。TF1函数是通过TH1和TGraph实现的。当然，选择不同的参数可以改变拟合方法，例如“L”使用对数似然法，“WL”使用加权对数似然法，以及“P”使用皮尔逊卡方法。最小二乘法的基本原理主要基于以下步骤：
首先选择（假设）一个模型函数，线性（例如
）或非线性形式（例如高斯分布函数） 分别计算每个数据点模型预测值与实际观测值之间的差值
通过微分或数值方法找到最小化目标函数的参数值:
最小二乘法具有一些独特的优势。首先它十分简单，计算量不大，计算时间较小；同时，它具有广泛的适用性。另外，如果数据满足高斯分布（假设），最小二乘法提供的估计是最优的（最小方差无偏估计），同时由于中心极限定理（在文章的后面会详细解释），当数据量特别大时，即使数据不严格满足高斯分布假设，最小二乘法的有效性仍然较高。或者说，在大样本的情况下，残差的分布趋于正态，最小二乘法仍能提供接近最优的估计。不过，效果的好坏还取决于数据偏离正态分布的程度和以及其他特殊情况。
正因为这一点，在选取是否选择TF1时（特别是当数据点不太多时）需要特别小心。首先，必须确保数据符合最小二乘法的假设，例如误差独立且服从正态分布。另外，还必须选择合理的模型，这样才能够相对更准确地拟合获得需要的或者合理的曲线。
另外，在上一次的任务中，我们调整了不同的bin大小，检查拟合的情况。在TF1拟合中，选择合适的bin数也是必要的。过多的bin会导致每个bin中的数据量减少，增加统计误差，特别是在数据点稀少的情况下，这可能导致拟合的不稳定性和不准确的参数估计，会太过关注数据的局部震荡或者导致过拟合；过少的bin会使得数据的细节信息丢失，无法准确反映数据的真实分布，使拟合结果过于粗糙，并可能掩盖重要的结构特征。
一般地，还需要注意拟合范围设置和拟合方法的选择。例如，使用”R”选项来指定函数的拟合范围，以确保拟合集中在数据的相关或者关键部分。对于低统计数据（泊松统计），使用对数似然法（选项”L”或”WL”）更合适；对于常规拟合（高统计量且误差iid），使用默认的最小二乘法即可。
最大似然法（或者极大似然法）是另一种统计方法，它的核心思想是找到一组参数，在这些参数下，观测数据出现的概率（似然）最大化。例如，假设有一组观测数据集
通过求解对参数
最小二乘法和最大似然法具有不同的应用场景：
- 最小二乘法假设误差独立同分布，通常为正态分布，目标是最小化观测值与预测值之间的误差平方和，常用于线性回归；最大似然法假设给定模型下数据的概率分布形式，目标是最大化数据在模型下的出现概率，它更一般化，适用于任意概率分布。
- 最小二乘法适合误差为正态分布且方差一致的情况，主要用于回归问题；最大似然法适合各种分布形式，广泛用于统计建模和机器学习。
- 最小二乘法具有更简单的计算过程，特别是线性模型有无可比拟的优越性（解析解）；而最大似然法的计算复杂度可能较高，特别是在多参数和非线性模型中，需要数值优化方法。
- 最小二乘法对异常值敏感，因为它最小化的是误差的平方，异常值影响较大；最大似然法的鲁棒性取决于误差分布的假设，如果假设合理，对异常值的鲁棒性会更好。
- 需要注意的是，两者在大样本下的估计结果趋同，MLE具有无偏性、一致性和渐近正态性，而最小二乘法是MLE在正态误差下的特例。
评价拟合质量有不同的方法。首先有几种简单的方法：
- 残差方差分析：观察拟合残差（即观测值与拟合值的差）的分布情况。理想情况下，残差应该为0。由于绝大多数情况未必理想，因此选择较小的残差统计可以选择较优的模型
- 卡方检验：较低的归一化卡方值通常表示拟合质量较好。在实际过程中，使用“单位自由度的卡方值”或“归一化卡方统计量”是一个相对较好的方法。卡方统计量除以自由度（
）能够衡量模型的误差或拟合度，能够表示每个自由度（或者每个参数）平均承担的误差或不匹配程度。如果 ，通常表示模型与数据拟合得很好，观测数据与期望数据的差异可以被认为是由随机误差引起的。如果 ，则表示模型拟合较差，存在较大的误差或偏差。反之，如果 ，通常表示模型可能过拟合数据，即模型可能过于复杂，精度过高，不仅拟合了数据的趋势，还拟合了数据中的噪声。 检验：衡量模型解释数据方差的比例，值越接近1表示拟合越好 - 置信区间和误差估计：检查拟合参数的置信区间和误差，较窄的置信区间和较小的参数误差表示拟合更可靠
- 预测区间：用于量化未来观测值落入某范围内的概率，反映拟合模型的预测能力
还有一些其它较复杂的方法。其中一个有效的方法是进行交叉验证（机器学习或者常规的拟合都可以用到），例如将数据集中的一部分作为训练集，一部分作为测试集，不断切换切分模式以及拟合的模型，直到寻找到某个对测试集而言最符合条件的模型，这可能就是较可靠的模型。通过这样验证，观察训练误差和测试误差，还能识别模型是否过拟合或欠拟合。
Task 2
2.1
在上一次任务中 ，我们介绍了轫致辐射：如果一个带电粒子在核的库伦场中剧烈减速，它的部分动能将以发射光子的形式损失，称为（库伦场中的）轫致辐射。轫致辐射这个过程通常发生在高速电子通过物质（如金属靶）的过程中。
轫致辐射本质上是一种特殊的、因粒子加速而产生的电磁辐射。直观上可以粗略地认为，当带电粒子向核子撞击（可能成一角度）时，如果能量不够大，会在近核的强库伦场中发生剧烈的减速过程，从而产生电磁辐射。
高能粒子由于轫致辐射而导致的能量损失由下式描述^[1]：
可以直观地看出，可以近视地认为电子的轫致辐射能量正比与粒子能量
其中，我们定义
具有
类似地，由这个微分方程可以得到
可以发现，当
在韧致辐射中，还有一个与辐射长度相关的概念，定义为临界能量
它被定义为例子的辐射损失和碰撞损失相等时的能量。当带电粒子的能量小于
比较它与辐射长度的近似公式可以发现，它们之间虽然没有直接的线性关系，但是都依赖于介质的原子序数
之前提到的韧致辐射实质上是带电粒子的电磁相互作用。对于粒子探测而言，粒子之间还有显著的强相互作用，尽管发生的距离相比电磁相互作用而言小一些。以质子-质子散射为例，在低能下，弹性和非弹性的截面都显现出相当强烈的能量依赖：
在非弹性过程中，和辐射长度类似，可以定义核作用长度，它实质上描述了强子在物质中的指数吸收：
需要注意的是，严格来说，强子界面依赖于能量，而且不同强相互作用粒子的截面有一些不同，但是就核相互作用长度与碰撞长度来说，两个截面总是与粒子种类无关。
在电子经过碳、铝、钨板的过程中，只需要考虑韧致辐射产生的能量损失（对应前文辐射长度），没有强子之间的相互作用（对应前文核反应长度）。
首先确定碳、铝、钨板对电子的辐射长度，分别为18.8 cm，8.9 cm，0.35 cm。使用公式
可以得到，在0.1 cm的过程中衰减率
可以很明显地发现，原子序数较大的粒子的相对衰减率确实更高。
多次库伦散射的散射角实际上由莫里哀理论描述。当散射角较小的时，它是围绕着其平均值
平面投影散射角的方均根为
其中，1GeV、10 Gev、100 GeV的高能电子有
而C，Al，W的
| C | Al | W |
|---|---|---|
| 7.9458E-04 | 1.1959E-03 | 6.9234E-03 |
| 7.9458E-05 | 1.1959E-04 | 6.9234E-04 |
| 7.9458E-06 | 1.1959E-05 | 6.9234E-05 |
如果是空间散射角，则乘以
| C | Al | W |
|---|---|---|
| 1.1235E-03 | 1.6911E-03 | 9.7897E-03 |
| 1.1235E-04 | 1.6911E-04 | 9.7897E-04 |
| 1.1235E-05 | 1.6911E-05 | 9.7897E-05 |
事实上，由于散射角分布的方均根与能量成反比，因此每一行只有数量级的差异。另外，由于涉及的电子具有极高能量，因此电子散射角分布的方均根的很小的数值具有合理性。
[Question：世界上有哪些加速器能达到这么大的加速结果？]
1 GeV级别：德国电子同步辐射源 (BESSY II)能够加速到约1.7 GeV的能量，波恩电子同步加速器 (ELSA)能够加速到最高约3.2 GeV的能量。
10 GeV级别：日本筑波高能电子-正电子对撞机 (KEKB)的设计能量为8 GeV的电子和3.5 GeV的正电子，美国电子同步加速器 (SLAC National Accelerator Laboratory)有一个可将电子加速到50 GeV的线性加速器，但在其不同的能量运行模式中可以将电子加速到10 GeV左右。
100 GeV级别：大型电子-正电子对撞机 (LEP)，设计能量为最高209 GeV（每束）（已在2000年停止运行）； 未来圆形对撞机 (FCC-ee)以及CEPC。另外，AMS已经探测到最高可达到TeV级别的电子能量，远高于100 GeV。这样的高能电子通常被认为来自极端天体物理现象，如超新星爆发、伽马射线暴、活动星系核等。
[Question：这里的偏转数量级是否合理？]
如何估计这里的数量级是否合理？
2.2
粒子穿过介质时，电离能量损失的分布受到介质厚度的影响主要可以分为两种情况。在薄介质中（通常指粒子穿过的路径长度远小于粒子平均自由程），能量损失的分布通常会呈现出类似的Landau分布；当粒子穿过厚介质（通常指粒子穿过的路径长度远大于粒子平均自由程），能量损失的分布往往趋近于Gauss分布。
首先可以对薄吸收层的情况做一个简要的解释。当带电高能粒子穿过物质时，它会通过几个竞争过程失去能量。对于快速重带电粒子（即粒子质量>>电子质量），能量损失的主要模式涉及到与材料电子的非弹性碰撞，导致材料原子的电离和激发（可能会使用Bethe-Bloch公式描述）。由于碰撞是离散且随机的，因此碰撞次数预计会出现统计波动。直观上，大的能量损失需要特殊的碰撞事件（例如特别近的粒子轨迹，或者很高的动能转移），特别是在碰撞次数与碰撞概率较小的情况下。事实上，高能区在近似下，这种高能事件发生的概率
这种分布可以用朗道分布加以参数化。朗道分布可以近似为
其中
就描述了上一段中提到的能损位置偏移，称为最可几能量损失。事实上，实际的能损失分布往往比朗道分布要宽。更恰当的描述方式是Vavilov修正的朗道分布（或者直接称为Vavilov分布），我们会在介绍完厚吸收层的情况后进一步解释。下图给出了朗道分布示意图，以及3 GeV电子在工作气体为
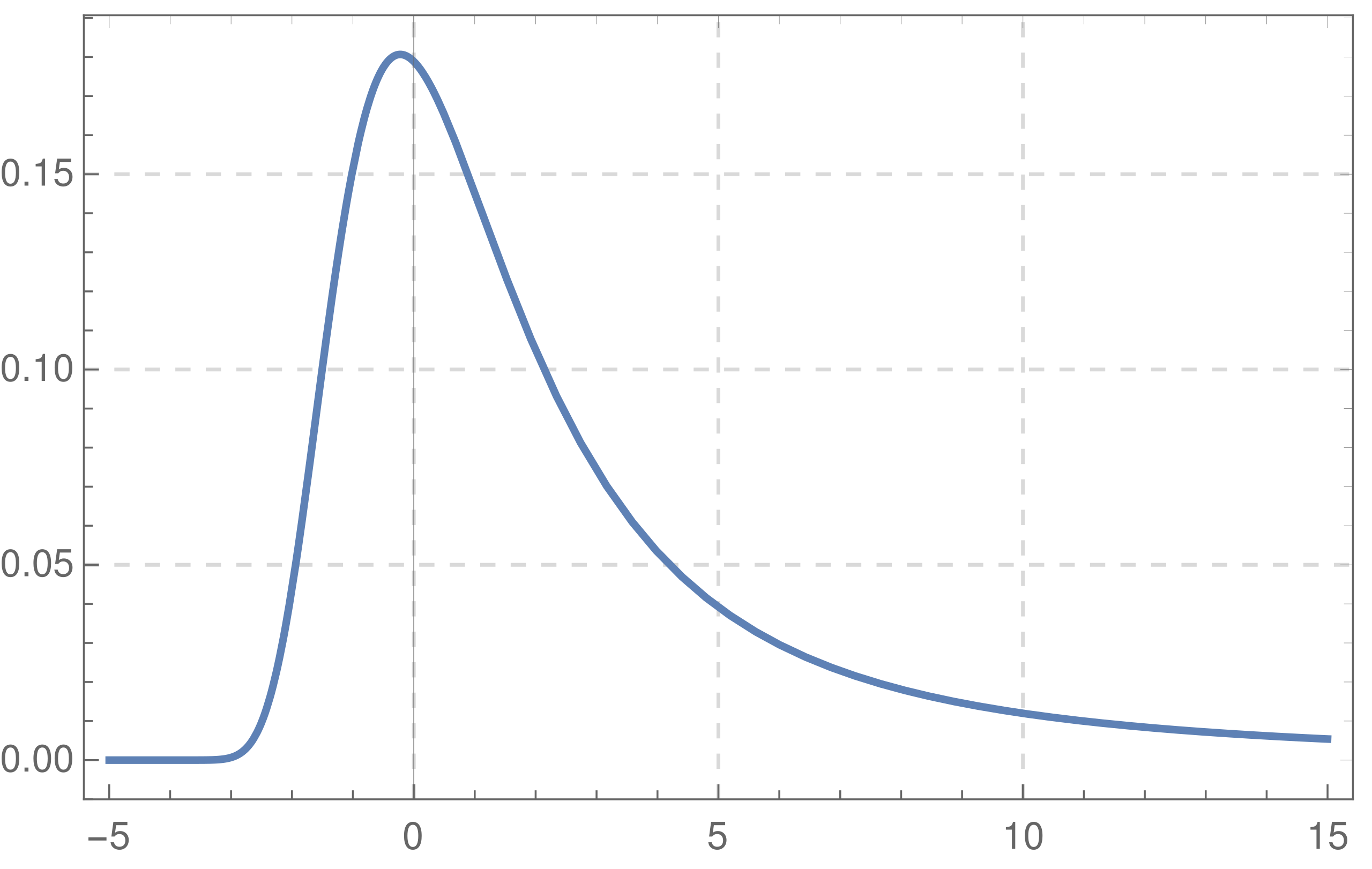
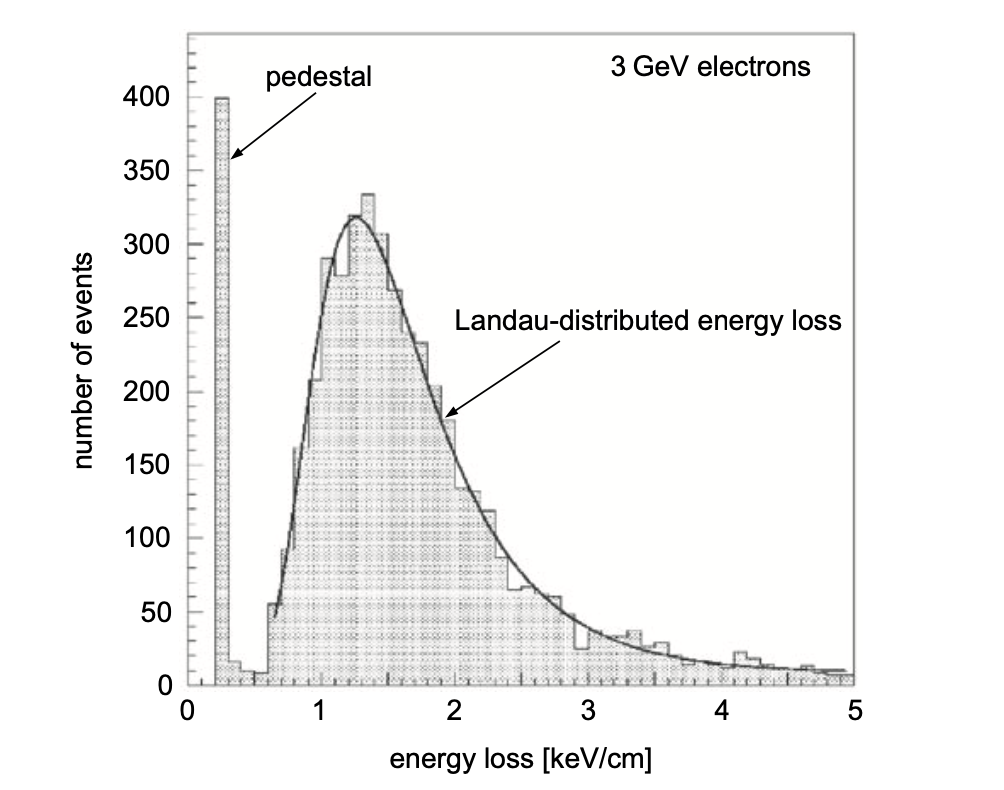
教材中给出了电离分布过程满足朗道分布条件（路径很短，例如薄层气体）：
与此对应，当
时，可以认为此时的吸收层为厚吸收层。对于厚吸收层，大能量的传递导致朗道分布的尾巴被压缩了。对于很厚的吸收体，能量损失分布可以用高斯分布作为近似。在厚吸收层中，带电粒子经历的碰撞次数显著增加，这导致能量损失的总量更接近于平均值，能量损失的分布也更加对称。在厚吸收层中，质子和其他重粒子主要通过电离过程失去能量；由于大量碰撞的累积效应，能量损失呈现出较小的波动幅度。
事实上，这可以用中心极限定理解释这一现象。对于一组iid的随机变量，它们平均值的分布会趋向于正态分布，无论这些随机变量本身的分布是什么，只要这些变量的方差有限，样本数足够大，样本均值的分布就会接近正态分布：
对于厚吸收层的情况，其中各次碰撞事件可以被看作是相互独立的，每次碰撞的结果不依赖于其他碰撞事件；每次碰撞所导致的能量损失可以认为来自同一概率分布（尽管具体形式可能较复杂）。所以，当吸收层足够厚时，碰撞次数足够大，即使每次碰撞的具体能量损失可能差异很大（随机变量的方差可能较大），但随着碰撞次数的增加，总能量损失分布会趋向一个正态分布（高斯分布）。这可以合理地解释厚吸收层必然具有趋于高斯分布的能量损失分布。
可以使用蒙特卡洛法模拟带电粒子在厚吸收层中的能量损失，为每个粒子设置不同的碰撞次数，这些碰撞次数表示粒子在穿越材料过程中与原子或电子发生的相互作用次数。为了更加直观，不妨使用指数分布来模拟每次碰撞造成的能量损失，它的长尾能够更明显地展示能量损失分布的非对称性：
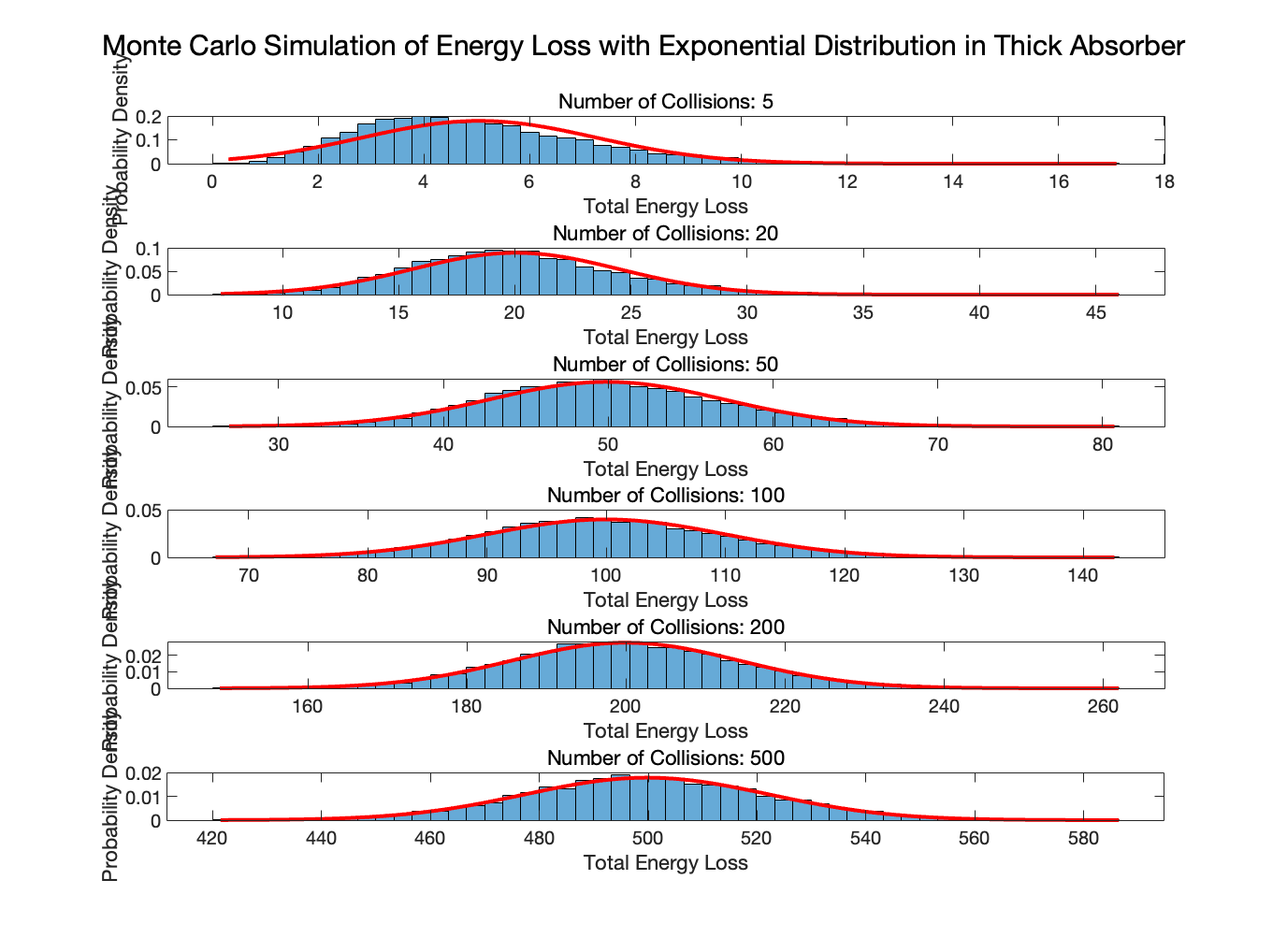
从图中可以明显地看到，在较少的碰撞次数下，总能量损失的分布保留了指数分布的特性，具有显著的长尾和不对称性。这是因为碰撞事件较少，能量损失的分布受到单次大能量损失事件的显著影响，导致偏态分布。随着碰撞次数增加，总能量损失的分布开始逐渐变得更加对称；虽然图像仍有一些偏态特征，但总体分布的形状开始趋向于高斯分布。最终，当碰撞次数进一步增加时，总能量损失的分布明显趋向于高斯分布。此时中心极限定理起作用，随着独立随机变量（碰撞）的数量增多，这些变量的和（总能量损失）趋向于正态分布，无论单个变量的分布形状如何。
论文[3]中给出了实验的直观结果：对于具有895MeV能量的氦离子，穿过0.057
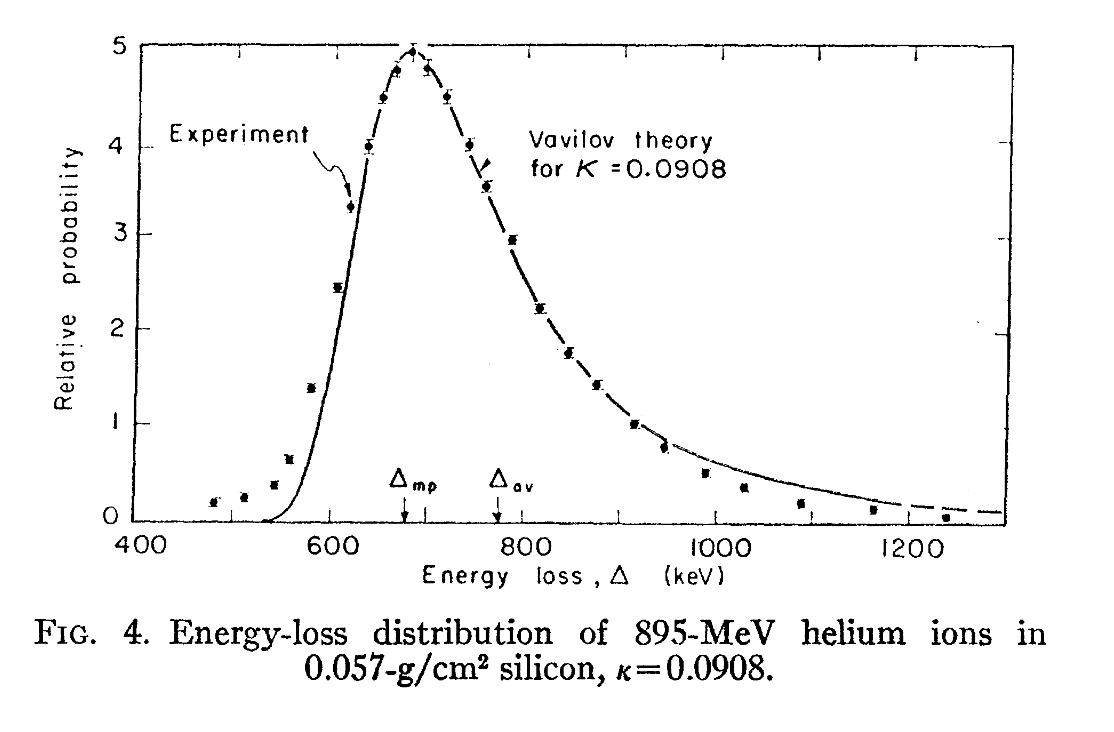
如果保持能量不变，将厚度增加一个数量级，发现偏态性明显地降低，得到一个更趋向于正态分布的结果：
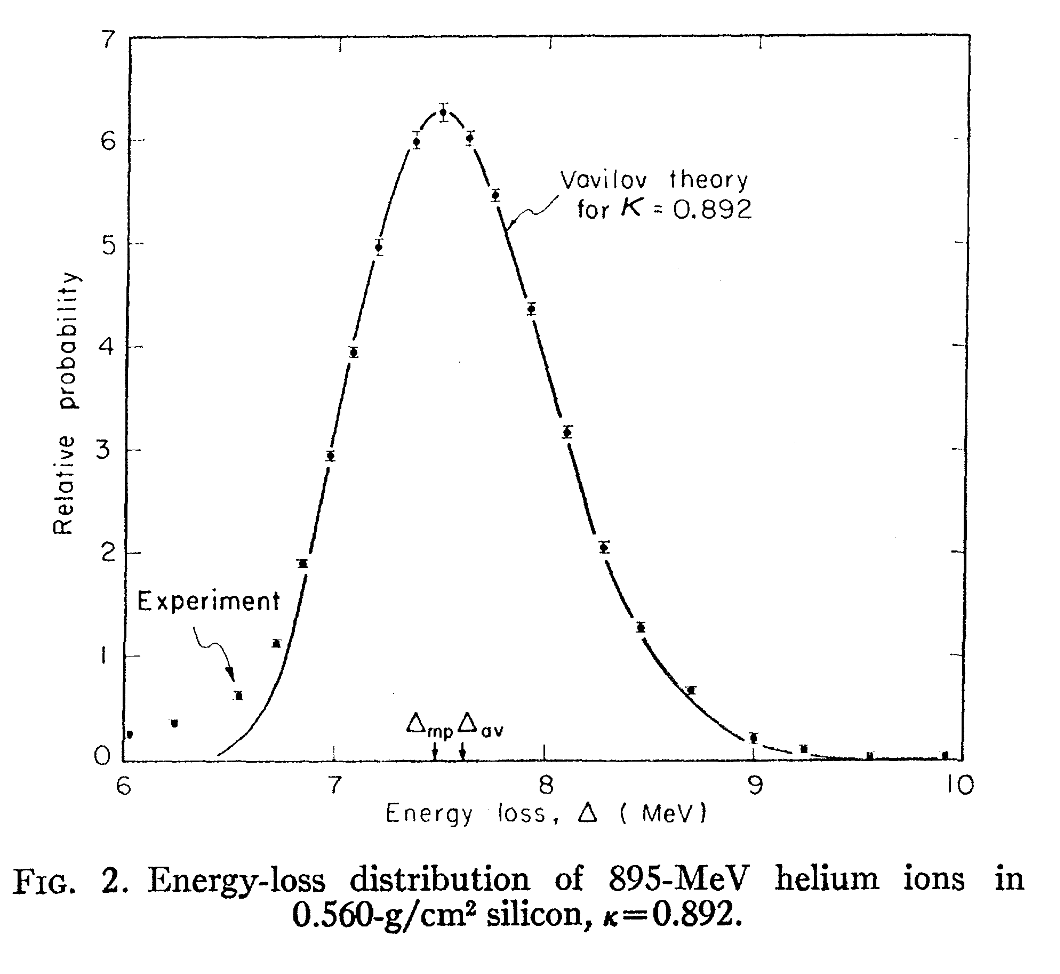
在另一种情况下，对于45.3MeV的质子，穿过0.265
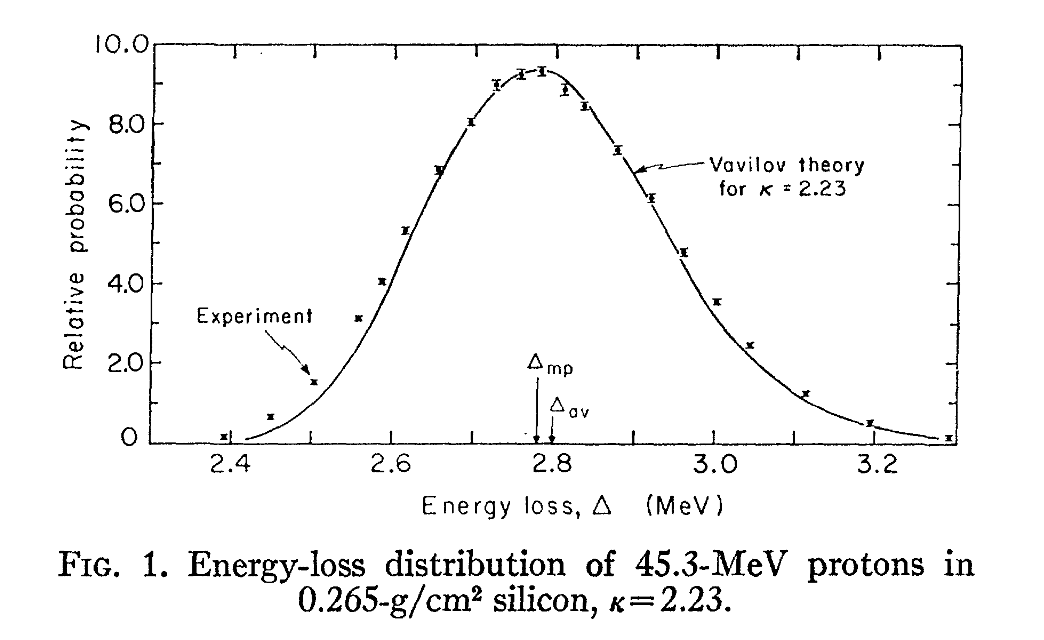
图中可以很清晰地表示他们之间的关系。
实际上，正如之前提到的，对于薄吸收层而言，实际的能损失分布往往比朗道分布要宽；更恰当的描述方式是Vavilov修正的朗道分布，它描述了吸收层厚薄程度介于两种之间的情况。Vavilov分布可以被看作朗道分布的推广，适用于描述中等厚度的吸收层中的能量损失分布。Vavilov引入了一个无量纲参数表征材料厚度与电子停止功率的比率：
其中
实际上它在数值计算中更常用。同样可以可视化它的变化：
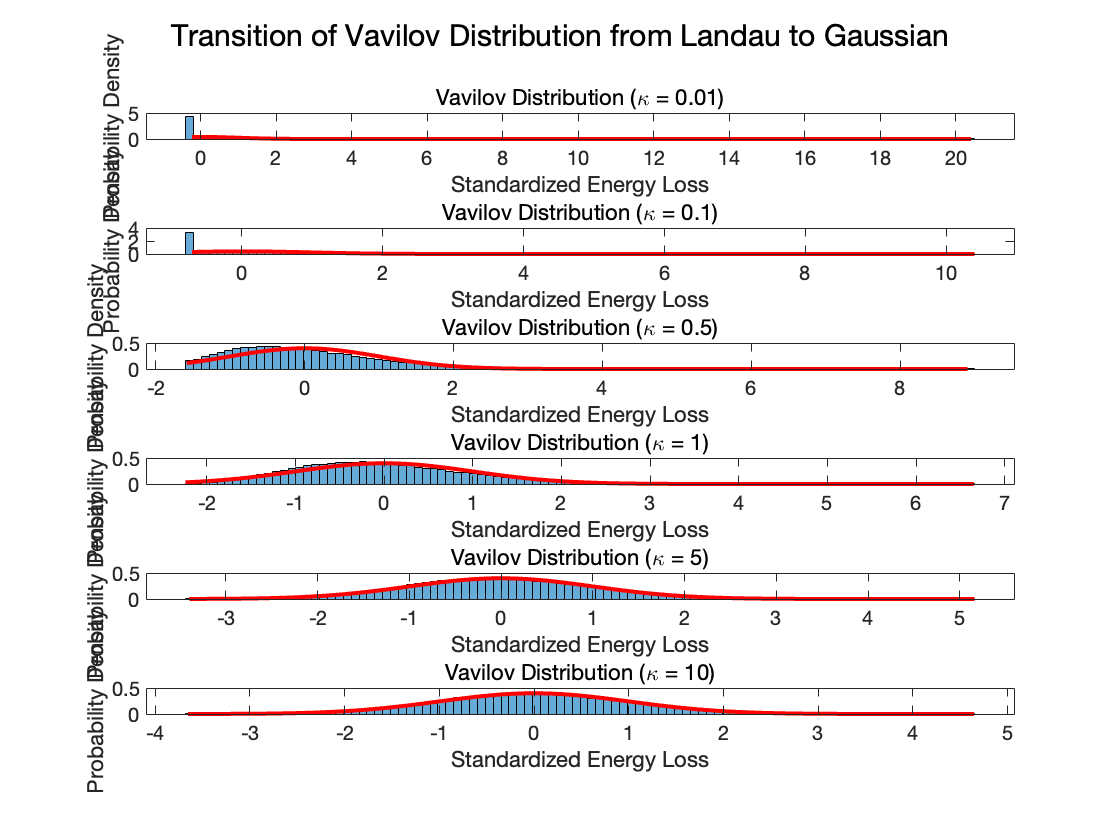
很明显地看出，当
参考文献
[1] B. Rossi, High Energy Particles, Prentice-Hall, Englewood Cliffs (1952)
[2] U. Amaldi, Fluctuations in Calorimetric Measurements, Phys. Scripta 23 (1981) 409–24
[3] H. D. MACCABEE, M. R. RAJU,* AND C. A. TOBIAS, Fluctuations of Energy Loss by Heavy Charged Particles in Thin Absorbers, PHYSICAL REVIEW (1968) 165-2
- Title: A&C_task 1.2
- Author: Albert Cheung
- Created at : 2024-08-20 21:53:27
- Updated at : 2024-08-26 19:29:40
- Link: https://www.albertc9.github.io/2024/08/20/2024A-Ctask2/
- License: This work is licensed under CC BY-NC-SA 4.0.
