A&C_Task 1.1

Albert Cheung
  2024-08-14 15:45:41 2024-08-14 15:45:41 Created   2024-08-20 16:39:08 2024-08-20 16:39:08 Updated      4.5k Words  15 Mins

Tasks

Task 1

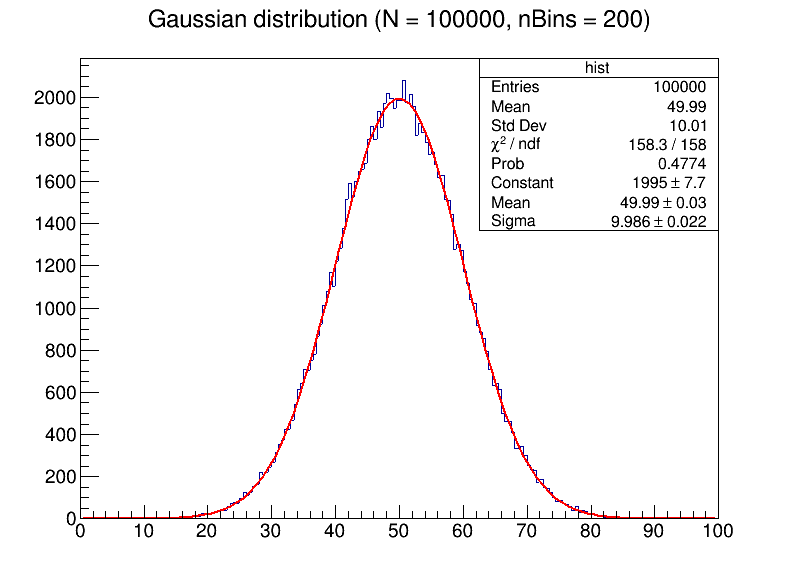
  1. 使用ROOT，生成数量为N的随机数，其服从均值为50，标准差为10的高斯分布。然后进行拟合，比较不同N与bin大小对拟合结果的影响。

Task 2

  1. 粒子产生电磁辐射的条件是什么？

  2. 直线加速器和环形加速器采用不同形状主要是基于什么考虑？

  3. CERN的FCC和CEPC直径各是多少？选择直径的主要考虑因素是什么？

One Possible Solution

Task 1

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <TFile.h>
#include <TH1F.h>
#include <TRandom3.h>
#include <TF1.h>
#include <TCanvas.h>
#include <TLegend.h>
#include <TPaveStats.h>
#include <iostream>

// 定义函数generate_and _fit_gaussian，用于生成数量为N，bin数为nBins的随机数据点
void generate_and_fit_gaussian(int N, int nBins) {

    // 使用TRandom3类型生成rnd随机数，以时间为seed
    TRandom3 rnd(0);

    // TH1F用于创建一维浮点型直方图。创建指针 '*hist' 以定位。使用Form以命名生成后直方图的标题。最后，设定了X轴的范围。
    TH1F *hist = new TH1F("hist", Form("Gaussian distribution (N = %d, nBins = %d)", N, nBins), nBins, 0, 100);
    
    // 生成服从高斯分布，均值为50，方差为10的数据点，存储在'double value'中；最后调用Fill，将前一步生成的随机数'value'填入直方图中。
    for (int i = 0; i < N; ++i) {
        double value = rnd.Gaus(50, 10);
        hist->Fill(value);
    }

    // 类似地，可以定义TF1类以表示一维函数，用于创建一个名为'gausFit'的高斯函数，用于后续的拟合操作。  
    TF1 *gausFit = new TF1("gausFit", "gaus", 0, 100);

    // 用静默模式用高斯函数拟合直方图数据
    hist->Fit(gausFit, "Q");

    // 创建一个800*600像素的画布对象，命名为"Gaussian Fit'；而后，在当前c1画布上绘制直方图
    TCanvas *c1 = new TCanvas("c1", "Gaussian Fit", 800, 600);
    hist->Draw();

    // 设置统计框和拟合参数的显示
    gStyle->SetOptStat(1111); 
    gStyle->SetOptFit(1111); 

    TPaveStats *stats = (TPaveStats*)hist->FindObject("stats");
    if (stats) {
        stats->SetX1NDC(0.6); 
        stats->SetX2NDC(0.9); 
        stats->SetY1NDC(0.6); 
        stats->SetY2NDC(0.9); 
    }

    c1->SaveAs(Form("/home/albert/rootdoc/ACtask1/GaussianFit_N%d_nBins%d.png", N, nBins));

    // TFile保存root文件
    TFile *outputFile = new TFile(Form("/home/albert/rootdoc/ACtask1/GaussianData_N%d_nBins%d.root", N, nBins), "RECREATE");
    
    hist->Write();
    outputFile->Close();
}

// 定义与文件名相同的函数，遍历不同数据点与分箱数；最后，会生成3*3种不同的情况。
void task1_1() {
    int Ns[] = {1000, 10000, 100000};
    int binSizes[] = {50, 100, 200};
    for (int i = 0; i < 3; ++i) {
        for (int j = 0; j < 3; ++j) {
            generate_and_fit_gaussian(Ns[i], binSizes[j]);
        }
    }
}

可以清晰地看到，当数据点较少的时候，如果过度增大bin的数目，将会使噪声十分明显，影响拟合的平滑性，使数据难以分析。随着数据点的增加，拟合出来的曲线更加贴近高斯分布，具有更小的误差。

生成的图像为

test
test
test
test
test
test
test
test
test

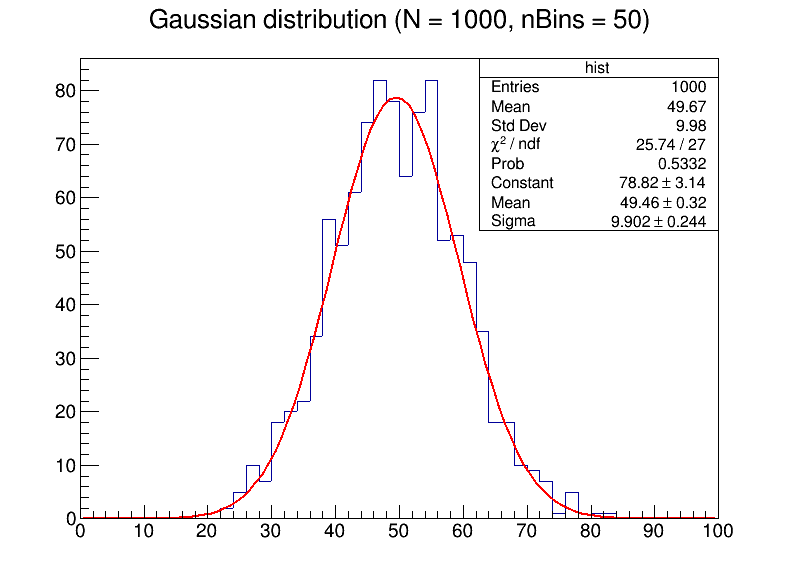
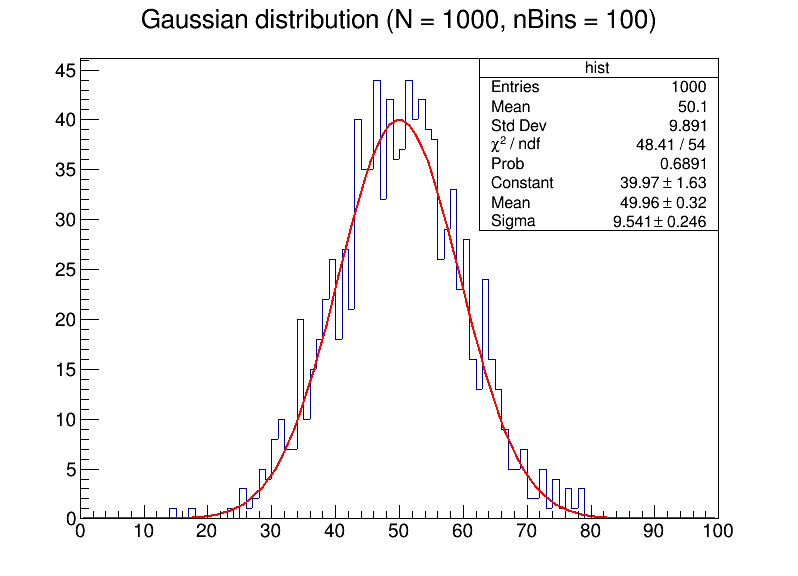
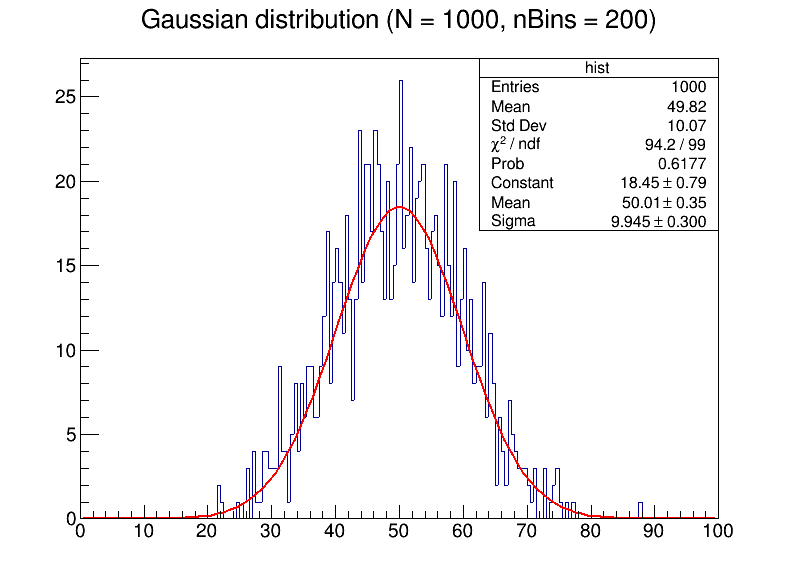
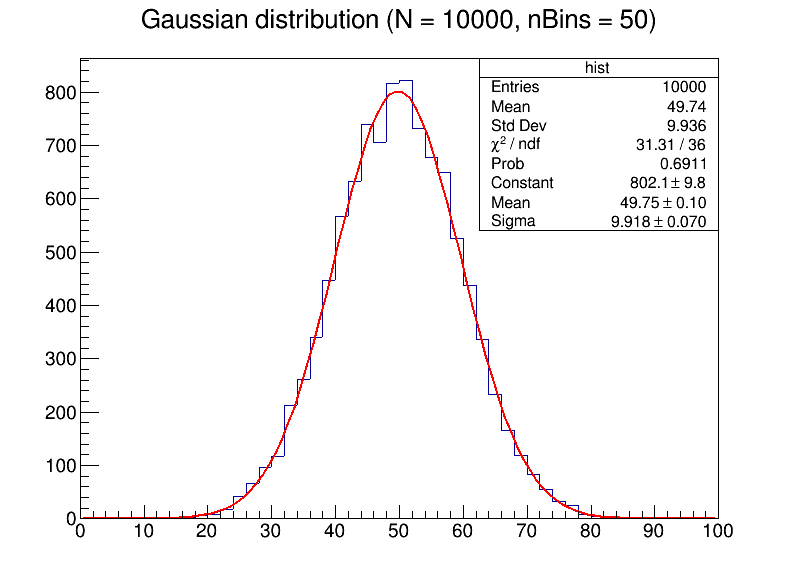
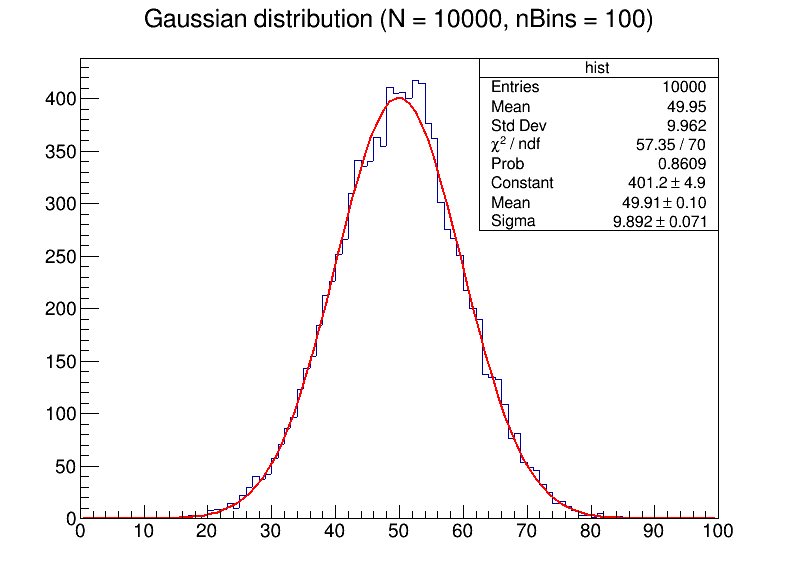
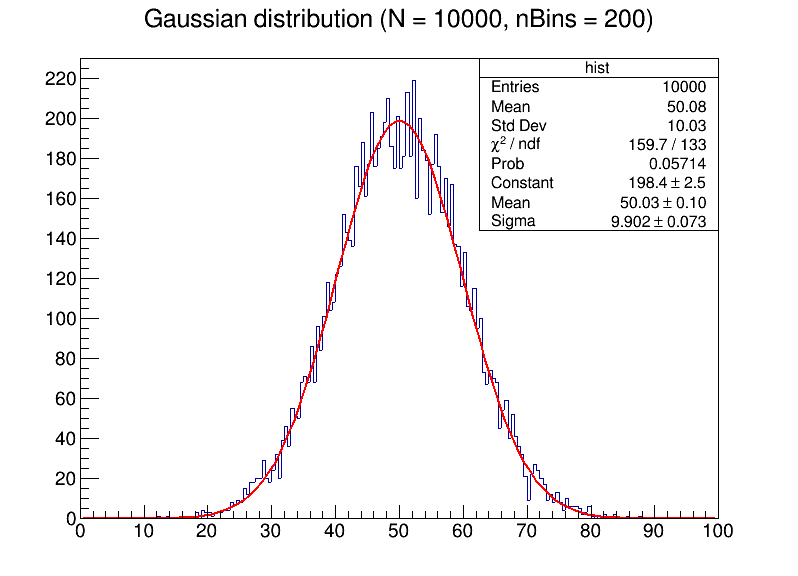
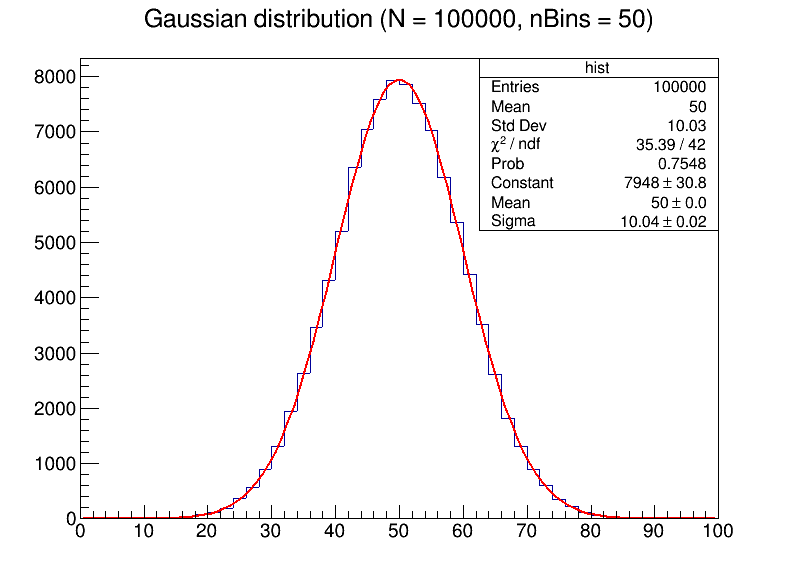
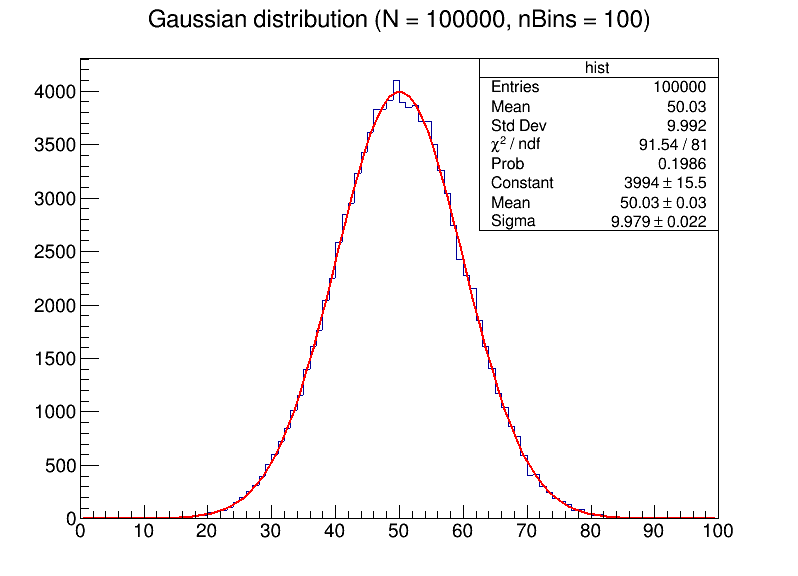
Task 2

1.1

粒子产生电磁辐射可能由于多种原因。具体如下：

  1. 加速运动

    任意带电粒子沿直线或曲线加速时将发射电磁辐射。此时主要分为两种情况：

    • 电子在直线加速器中加速时产生辐射。直线加速辐射通常在较低的频率范围内，损失能量较小，方向性较弱。
    • 电子在环形加速器（例如同步加速器或回旋加速器）中加速时产生同步辐射。同步辐射可以被看作是磁轫致辐射的一个特殊过程。同步辐射具有强烈的方向性，通常覆盖从无线电波到X射线的广泛频率范围，高能粒子甚至能够产生非常高频率的X射线和伽马射线。它主要集中在切线方向上，集中性与粒子能量正相关。因此，高能电子的加速器必须采用直线型加速器。

  2. 轫致辐射

    带电粒子在核的库伦场中剧烈减速，它的部分动能将以发射光子的形式损失，称为轫致辐射。如果带电粒子在磁场中发生偏转，会发射同步辐射光子，称为磁轫致辐射。环形加速器中的同步辐射是一种特殊情况。轫致辐射具有临界能量，大于临界能量的情况下产生率显著增加。轫致辐射可能产生能谱很宽的射线或X射线。

    轫致辐射本质原因和上一条中的由于加速运动而产生的电磁辐射十分类似；或者说，轫致辐射是一种特殊形式的因粒子加速而产生的电磁辐射。其特殊点主要在于轫致辐射主要指的是在靠近核时受到强烈的库伦场的剧烈减速而产生电磁辐射，这导致了它释放的电磁辐射主要集中在伽马射线和X射线的频段，通常具有很高的能量。这个过程通常发生在高速电子通过物质（如金属靶）的过程中。

    在一些资料中，习惯将由核产生的强库伦场导致的轫致辐射简称为轫致辐射，而将由带电粒子在磁场中偏转产生的轫致辐射单独称为磁轫致辐射。这两种轫致辐射其实都是由于粒子具有强烈的加速度而产生的电磁辐射，其中一种是剧烈的减速引起的，而另一种由于剧烈的偏转（或者说强烈的向心加速度）。如果粒子在同步加速器中的同步磁场中进行加速，我们称此时的磁轫致辐射为同步辐射。同步辐射会产生极高频的X射线射线，可能会损失相当大的能量，这在加速电子等轻子时尤其明显。因此，在目前的技术里，如果想将电子加速到100GeV能区以上，必须利用直线加速器，或者建造具有相当大的直径的加速器（例如CEPC）。

  3. 在介质中的超光速运动

    如果带电粒子在介质中运动的速度超过该介质中的光速时，会产生切伦科夫辐射。这种辐射对能量损失的贡献相比电离与激发要小得多，它是由于粒子在介质中产生的电磁场无法及时被介质的极化所屏蔽而形成的前向辐射。

    一般来说，当粒子在介质中进行较低速度的匀速运动时，不会产生电磁辐射。这是因为，当粒子在介质中的飞行速度小于介质的光速时，带电粒子会使路径周围的原子发生极化而成为电偶极子，它们具有完整的对称性，电偶极场的积分恒为0；然而，当带电粒子在介质中以大于介质光速的速度飞行时，会导致对称性被破坏，产生不为0的偶极矩，从而产生切伦科夫辐射。具体来说，当粒子的移动速度小于介质中的光速时，其产生的电场扰动传播速度比粒子的运动速度快，从而极化容易及时地弥散开来，极化和退极化的过程局部且瞬时，保持了电偶极场的积分恒为0，不会产生任何相干的波阵面，因此不会产生宏观可观测的电磁辐射；而当粒子的移动速度大于介质中的光速时，会导致介质中的极化效应无法及时消退，这时粒子的极化波前方会积累一个无法消退的极化“波阵面”，这些强烈、有序、集中、相干的波前就会导致电磁辐射的产生。

    这一过程可以简单地类比超音速飞机产生音爆的过程。当飞机超过音速时，声波无法在其前方传播，导致声波在飞机前方累积，形成冲击波，这种冲击波以音爆的形式释放能量。同样地，切伦科夫辐射是带电粒子超介质光速运动引起的电磁扰动以相干的电磁波形式释放的能量，和音爆过程十分类似。

    切伦科夫辐射的原理在许多方面具有重要的应用。首先的应用之处就是粒子计数器（切伦科夫计数器）。当高速粒子穿过介质时，它会发出不同类型的切伦科夫光，通过分析这些光可以判断粒子的速度和方向，这个技术在AMS-02和LHC中被广泛地应用。另外，切伦科夫辐射还可以用于粒子鉴别，通过已知的能量或者动量关系，可以通过前述的原理检测出它的能量。

  4. 散射过程

    对于某些非弹性散射，可以视为产生了新的光子（电磁辐射）。例如康普顿散射、拉曼散射和布里渊散射。这些过程实际上并不涉及光子的湮灭与再生，但由于其涉及了光子发射方向与能量的变化，因此可以在某种程度上视为电磁辐射的发射。实际上，这也不是带电粒子直接产生电磁辐射的过程。

  5. 跃迁过程

    在原子或原子核内部，粒子（电子或核子）从高能级跃迁到低能级时，能量以光子的形式释放出来，发射电磁辐射。带电粒子穿越物质时由于束缚电子的激发和电离会损失动能，导致低能光子（辐射）的产生：

    其中，在激发过程中，粒子通常会通过从高能级跃迁回低能级来释放多余的能量，这个跃迁过程会产生电磁辐射，通常以光子的形式出现。在电离过程中，离子可能也会回到较低的能态，产生电磁辐射；在一些情况下，电离过程可能会直接产生高能量的光子，这与散射过程相关。跃迁过程在粒子物理中常伴随着其它过程出现，例如散射、电离等，存在十分广泛。

    需要注意的是，在一些俄歇电子发射后，可能会产生次级X射线，这也属于跃迁过程。不过它本身与俄歇电子发射无关。

  6. 湮灭辐射

    当粒子和它的反粒子相遇并湮灭时，它们的质量会转换为能量，通常以光子的形式释放。例如，当电子和正电子湮灭时，会产生两个能量为511 keV的光子：

    在研究湮灭过程（湮灭辐射）时，可以注意以下几点：

    • 通过测量光子的能量，可以间接得到湮灭粒子对的质量
    • 由于动量守恒，通过测量光子的来向，可以确定事件发生的位置
    • 粒子的极化还可能会导致光子的极化

    湮灭过程可能会产生一些微小的不对称性，这要求对湮灭过程的精细测量。这可能是未来研究物质与反物质关系的重要手段。

  7. 等离子体辐射

    在等离子体中，带电粒子之间的相互作用（如集体振荡、电子-离子碰撞）也会导致电磁辐射。例如，等离子体振荡可以引发电磁波的发射，这种辐射在天体物理和等离子体物理中扮演了重要地位。

  8. 穿越辐射

    当带电粒子穿过介电性质不同的不同介质界面的时，会产生穿越辐射。简单来说，这是因为带电粒子和产生的镜像电荷产生偶极子电场在粒子穿越界面后突然消失，导致了电磁辐射的发射。它的影响相比带电粒子的总能量以及其它的能量损失而言小到可以忽略。需要注意的是，穿越辐射光子数正相关与粒子的能量（依赖效应），而前面提到的切伦科夫辐射依赖于速度，这导致它对相对论性粒子（或者说高能粒子）的鉴别比基于切伦科夫辐射的计数器的鉴别更有优势。这是因为相对论性粒子的增加相比膨胀而言不太明显的原因。

1.2

能量损失上：直线加速器中不存在同步辐射，损失能量较小；环形加速器会产生同步辐射，有时能够产生极高频的X射线或伽马射线，损失能量较多。因此，高能电子加速器（例如GeV）必须采用直线型加速器。必须提到的是，由于同步辐射，在加速高能粒子（特别是电子等轻子时），必须权衡辐射损失的能量和加速器提供的能量。由于辐射能量损失正比于，每四倍的直径提升才能抵消能量升高一倍带来的辐射损耗。例如，在设计CEPC时，使用100km的设计周长就是考虑到了电子的辐射能量损失，它的周长设计和目标加速能量是紧密相关的。在以前，如果想将电子的能量提高到100GeV以上，必须使用直线加速器；而希格斯玻色子的质量约为125GeV，只有在CEPC这样的大周长对撞机中才能获得足够得到希格斯玻色子的能量。另外，它为运行大致十年后，升级为超级质子对撞机，探索更高能量尺度提供了条件。

加速模式上：粒子在直线加速器中一般在每通过一段加速腔时被加速，因此要得到高能粒子，每段加速腔必须具备足够的电场强度；环形加速器在每圈轨道上经过多次相同的加速腔，因此可以逐步提高能量。这使得在特定能量范围内，环形加速器更为高效。不过需要注意的是，质子能达到的最大能量目前受到同步加速器中主导磁场强度的限制，以及可利用的同步加速器的限制。在现有的设备中，利用大的偏转半径和超导磁铁可将质子加速并存储到10 TeV能区。

粒子类型上：能量损失中提到同步辐射是能量损失上的严重问题。因此对于需要极高能量的轻子（例如电子），必须使用直线加速器；对于较重的粒子（例如质子、重离子），可以使用环形加速器。它们的同步辐射损失较少，而且可以逐步加速逐步提升能量。

另外，还有一些其它因素。例如，直线加速器通常需要较大的空间，而环形加速器可以建在有限的地下隧道内，节省了占地面积。另外，直线加速器在束流上比环形加速器更具备优势，而环形加速器可以通过多次尝试提高对撞的发生次数，同时产生的是双向的粒子流，能够提高对撞能量，例如LHC。

1.3

根据https://fcc-cdr.web.cern.ch/#intro 与 http://cepc.ihep.ac.cn/intro.html 的最新介绍，FCC和CEPC都具有100km的设计周长。

相比之前的对撞机或加速器，它们在周长上都具有很大的提升。例如，LHC和LEP都只具有约27公里的周长。周长（直径）的选择具有以下参考因素：

  1. 有效缓解了前述同步辐射损失的问题，有效提高了轻子的加速效率。在之前的段落中提到，同步加速器中加速轻子时可能会产生明显的磁轫致辐射（同步辐射）。FCC计划获得高达100TeV的碰撞能量，而CEPC计划获得100GeV量级的正负电子能量（240GeV）以达到能够产生希格斯玻色子的量级，拥有较长的周长（或者直径）能够有效缓解由于同步辐射产生的能量损失对加速的阻碍，从而使粒子的对撞能量达到一个新的量级。

  2. 更大的周长意味着更大的加速能量。FCC希望建造一个能够达到100TeV的质子-质子对撞机，而CEPC的第一阶段计划用于电子和正电子在240 GeV能量下的碰撞，探索希格斯玻色子的性质。同时，它相对而言降低了要求的磁场大小，也为获得更高能量的粒子增加了可能。

  3. 周长的设计同样考虑了成本。前文提到，每四倍的直径提升才能抵消能量升高一倍带来的同步辐射损耗。因此，必须权衡能量提高与周长提升需要耗费的成本之间的关系，只需要使粒子加速后得到的能量达到所要求的范围即可。

  4. 客观条件并不允许直径过度扩大。大型加速器或对撞机必须建造在合适的地理位置，例如要求具有花岗岩地质以节约造价。同时，隧道还需要埋在地下约50-100m处，以不影响地面建筑。另外，它还受限于交通的影响。

  5. 另外，将轨道加速器的尺寸提高到100km的数量级，可能需要考虑地球的曲率或者尺寸。如果继续提高尺寸，就会不可避免的遇到这样的问题。

  • Title: A&C_Task 1.1
  • Author: Albert Cheung
  • Created at : 2024-08-14 15:45:41
  • Updated at : 2024-08-20 16:39:08
  • Link: https://www.albertc9.github.io/2024/08/14/2024A-Ctask1/
  • License: This work is licensed under CC BY-NC-SA 4.0.
推荐阅读
A&C_task 1.2 A&C_task 1.2 A&C_task 1.3 A&C_task 1.3 Python基础入门 Python基础入门
推荐阅读
A&C_task 1.2 A&C_task 1.2 A&C_task 1.3 A&C_task 1.3
On this page
A&C_Task 1.1
  1. Tasks
  2. One Possible Solution