三维欧氏空间中的矢量与张量
张量的定义
张量可以被写为
或者缩写为
只要在一个坐标系中给出分量,同时给出坐标变换时分量的变换规律,就能定义一个与坐标系的选择无关的客观物理量,这就是定义张量的方法。
张量按它的角标数来分类,有n个角标的张量叫n阶张量。一个n阶张量的完整定义包括在一个坐标系中给出3n个数,以及规定这些数在坐标变换时的变换规律两部分。
矢量代数
坐标基矢
将坐标基矢定义为
定义二阶对称符号
定义三阶完全反对称符号
有
点积与叉积
首先规定,凡是进行了作和的角标称为哑标。哑标实际上并不取任何特定的值,而是取遍 1、2、3 三个值。在进行作和以后,哑标不再存在。反之,不作和的角标称为自由标。任何等式左、右两边的自由标必须正好对应。需要注意,当两和式相乘时,哑标不能重复。
注意一个规则:如果在一个式子的某一项中,含有因子
点积与叉积有
首先是利用
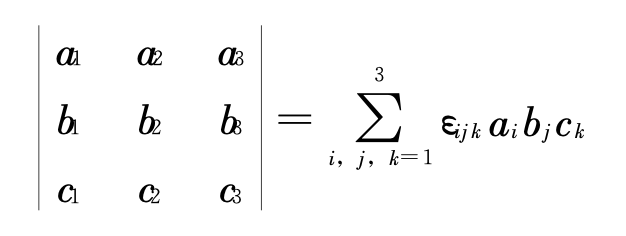
还有一个将
三矢量的连乘积
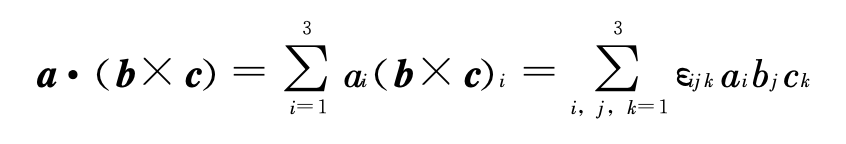
坐标变换
基矢的变换
有
即
以及
赝矢量与赝标量
在坐标反演时要改变方向的矢量叫做赝矢量;如果一个真矢量和一个赝矢量点乘,则所得到的数只在转动下不变,而在反演时要改号,这样的数称为赝标量。
赝矢量的坐标变换
对于赝矢量,坐标变换有
这说明,赝矢量的分量在坐标转动时和坐标基矢一样地变换,而在坐标反演时和坐标基矢的变换相差符号。
正交变换
以上所讨论的几种坐标变换(转动、反演和镜面反射)都保持矢量点积的公式不变,即
这样的变换称为正交变换。注意到正交变换由点积定义,因此如果在未定义点积的空间中不存在正交变换。
正交变换的变换矩阵必须是正交矩阵:
或者
可以发现,正交矩阵的不同行所代表的矢量相互正交,而每一行所代表的矢量长度1;类似地,正交矩阵的不同列所代表的矢量相互正交,而每一列所代表的矢量长度1。
三维欧氏空间中张量的定义
三维欧氏空间
矢量点积具有如下形式的空间称为(真)欧氏空间:
张量的定义
在坐标系
时,它按
变,则称它为一阶张量。如果它在坐标反演时变号,则称为一阶赝张量。
在任一坐标系中给出具有两个下标的9个数,当坐标变换时,这两个下标分别独立地按照和坐标单位矢量的变换规律相同的规律进行变换,则这9个数构成一个二阶张量。如果所给的9个数在坐标反演时,除了两个下标分别独立地按照和坐标单位矢量的变换规律相同的规律变换之外,还要改号,则得到的是二阶赝张量。
二阶张量分量变化规律为
高阶张量的定义和变化规律和二阶张量类似。在任一坐标系中给出具有
则这些数
一阶和二阶张量的整体符号
记
为一阶张量的整体符号;记
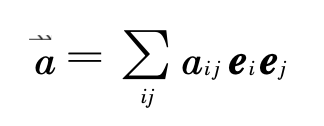
需要注意的是,上式右边并排书写的两个矢量
由整体符号求分量
类似地,由二阶张量的整体符号求分量
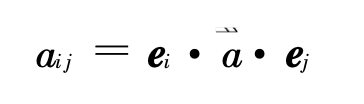
一个重要的二阶张量是
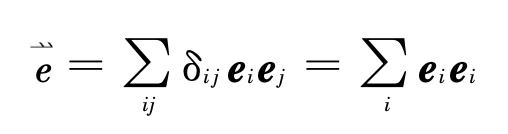
它和任意矢量
三维欧式空间中的张量运算
张量的运算
- 张量的加法
只有阶数相同的张量才可以相加:
- 张量的乘法
张量的乘积得到一个更高阶的张量,乘积阶数等于二者的阶数之和:
张量乘法的最简单例子是两个一阶张量相乘得二阶张量。设有两个矢量
是一个二阶张量,称为
- 张量的缩并
设有一个二阶以上的张量
则
- 指标的置换
将一个张量的任意两个下标的位置进行互换,仍然得到一个张量。这样的运算称为指标的置换。
三阶完全反对称赝张量
在任意坐标系中都按如下定义
的
三维欧氏空间中的二阶张量
如
称为二阶对称张量;如
称为二阶反对称张量。
对任意张量,总可以展开成对称部分和反对称部分
其中
需要注意的是,反对称二阶张量实质上等同于一个赝矢量。
二阶张量有一些不变量。有时在实际问题中这些不变量有重要的物理意义。
设有一个二阶张量
这就是张量
另一个不变量是
矢量场与张量场 梯度 散度 旋度
导数张量
设有一个
这是一个
梯度 散度 旋度
标量场的梯度为
或者用简写符号
矢量场的散度为
或者用简写符号
矢量场的旋度为
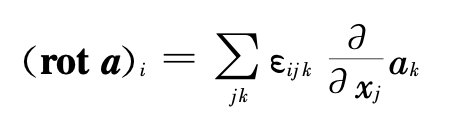
或者用简写符号
另外,有公式
- Title: 三维欧氏空间中的矢量与张量
- Author: Albert Cheung
- Created at : 2024-08-01 10:08:11
- Updated at : 2024-08-03 18:05:32
- Link: https://www.albertc9.github.io/2024/08/01/tensor-analysis-1/
- License: This work is licensed under CC BY-NC-SA 4.0.

