The particle physicist's view of Nature and Lorentz transformation

The particle physicist’s view of Nature

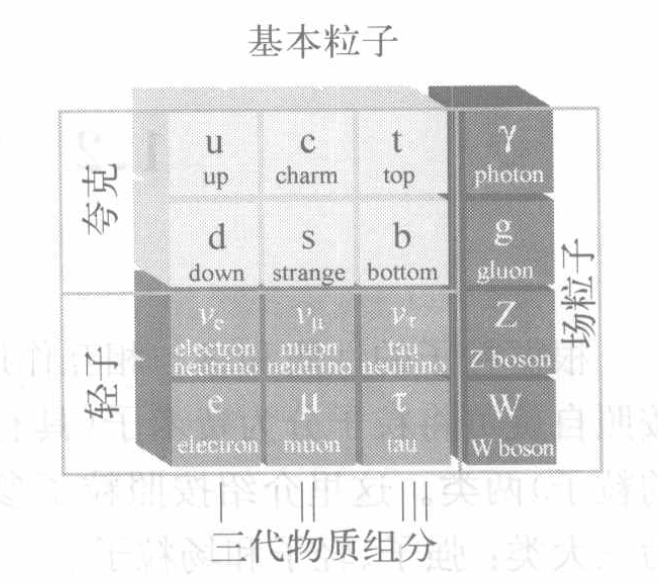
A short category of the particle on the Standard Model picture:

1 Elementary Particles:

1.1 Fermions

a. Quarks: up, down, charm, strange, top, bottom quarks; spin=1/2

b. Leptons: , , , , , ; spin=1/2

1.2 Bosons

a. Photon (); spin=1

b. and Bosons; spin=1

c. Gluon; spin=1

1.3 Higgs Boson

a. Higgs Boson; spin=0

2 Composite Particles

2.1 Hadrons

a. Baryons: Proton (), Neutron (),
and other strange baryons

b. Mesons: Pions (, , ),
Kaons (, , , ),
and other mesons

Supplementary formula

Electron-positron annihilation cross section:

where is the square of the centre of mass energy, the fine-structure constant. Also, define

In units, set . Remember:

Lorentz transformations

Rotations, boosts and proper lorentz transformation

Rotation:

Translation:

or

where .

Introduce general Lorentz transformation

where the matrices form a group called te proper Lorentz group (remember Einstein summation convention).

Define the interval as

and it is invariant under Lorentz transformation. Introduce metric tensor:

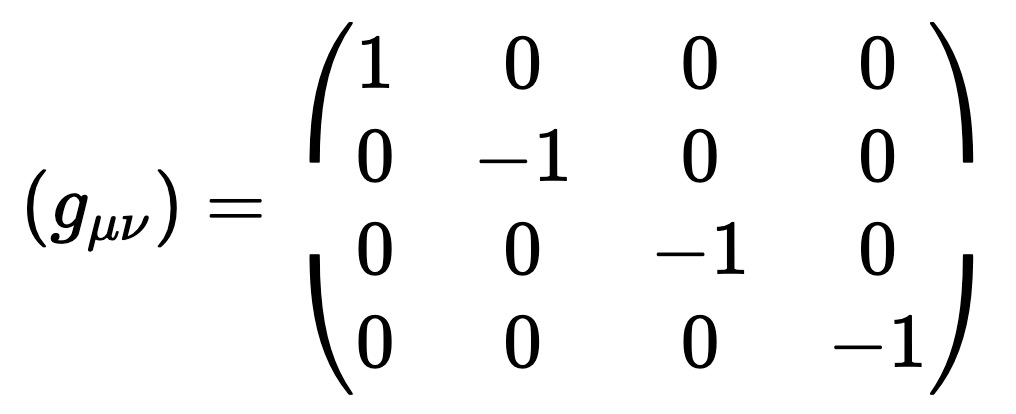
Then

Scalars, contravariant and covariant four-vectors

Scalar

Quantities which are invariant under Lorentz transformation are called scalars.

Contravariant Four-Vectors

Define a contravariant four-vector to be a set which transforms like the set under a proper Lorentz transformation:

an example is the energy-momentum vector of a particle .

Define a contravariant mertic tensor :

.

Covariant Four-Vector

Define the corresponding covariant four-vector, carrying a subscript rather than a super script, by

If , then .

We can write the invariant as

Scalar Product

More generally, in scalar product, if and are contravariant four-vectors:

is invariant under a Lorentz transformation.

Transformation Law for Covariant Vectors

Note that, different from , in general.

Also, using the invariance of the scalar product, we have

and

So, it follows that

Fields

Scalar Fields and Vector Fields

Define a scalar field

Then construct a vector field from a scalar field

Contravariant Vector and Covariant Vector

Define a covariant vector

Define the contravariant vector

following that

and

are invariant under Lorentz transformations.

Tensors

Tensors like , , , etc. can be defined as quantities which transform under a Lorentz transformation in the same way as , , etc. For example, define

The Levi-Civita tensor

The Levi-Civita tensor is defined by

, if is an even permutation of 0,1,2,3;
, if is an odd permutation of 0,1,2,3;
, otherwise.

And, satisfies

The corresponding Levi-Civita symbol in three dimensions is useful in the construction of volumes:

Similarly, the Levi-Civita tensor in four dimensions enables one o construct four-dimensional volumes by .

In particular, it can define the “volume” element of space-time:

which is a Lorentz invariant scalar.

Time reversal and space inversion

The operation of time reversal:

,
, .

The operation of space inversion:

,
, .

Note that is invariant, but these transformations are excluded from the proper Lorentz group.